Let  be a triangle with circumcircle
be a triangle with circumcircle  and incentre
and incentre  . A line
. A line 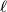 intersects the lines
intersects the lines 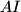 ,
, 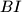 , and
, and 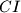 at points
at points  ,
,  , and
, and  , respectively, distinct from the points
, respectively, distinct from the points  ,
,  ,
,  , and
, and  . The perpendicular bisectors
. The perpendicular bisectors  ,
,  , and
, and  of the segments
of the segments  ,
,  , and
, and 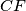 , respectively determine a triangle
, respectively determine a triangle 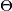 . Show that the circumcircle of the triangle
. Show that the circumcircle of the triangle 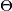 is tangent to
is tangent to  .
.
Let $ABC$ be a triangle with circumcircle $\omega$ and incentre $I$. A line $\ell$ intersects the lines $AI$, $BI$, and $CI$ at points $D$, $E$, and $F$, respectively, distinct from the points $A$, $B$, $C$, and $I$.
The perpendicular bisectors $x$, $y$, and $z$ of the segments $AD$, $BE$, and $CF$, respectively determine a triangle $\Theta$.
Show that the circumcircle of the triangle $\Theta$ is tangent to $\Omega$.
 be a triangle with circumcircle
be a triangle with circumcircle  and incentre
and incentre  . A line
. A line 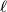 intersects the lines
intersects the lines 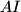 ,
, 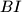 , and
, and 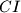 at points
at points  ,
,  , and
, and  , respectively, distinct from the points
, respectively, distinct from the points  ,
,  ,
,  , and
, and  . The perpendicular bisectors
. The perpendicular bisectors  ,
,  , and
, and  of the segments
of the segments  ,
,  , and
, and 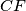 , respectively determine a triangle
, respectively determine a triangle 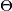 . Show that the circumcircle of the triangle
. Show that the circumcircle of the triangle 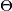 is tangent to
is tangent to  .
.  Školjka
Školjka