Let  be the circumcentre, and
be the circumcentre, and  be the circumcircle of an acute-angled triangle
be the circumcircle of an acute-angled triangle  . Let
. Let  be an arbitrary point on
be an arbitrary point on  , distinct from
, distinct from  ,
,  ,
,  , and their antipodes in
, and their antipodes in  . Denote the circumcentres of the triangles
. Denote the circumcentres of the triangles 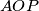 ,
, 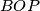 , and
, and 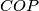 by
by 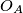 ,
, 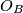 , and
, and 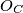 , respectively. The lines
, respectively. The lines 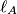 ,
, 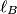 ,
, 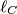 perpendicular to
perpendicular to  ,
,  , and
, and  pass through
pass through 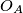 ,
, 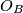 , and
, and 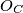 , respectively. Prove that the circumcircle of triangle formed by
, respectively. Prove that the circumcircle of triangle formed by 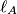 ,
, 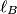 , and
, and 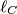 is tangent to the line
is tangent to the line 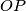 .
.
Let $O$ be the circumcentre, and $\Omega$ be the circumcircle of an acute-angled triangle $ABC$. Let $P$ be an arbitrary point on $\Omega$, distinct from $A$, $B$, $C$, and their antipodes in $\Omega$.
Denote the circumcentres of the triangles $AOP$, $BOP$, and $COP$ by $O_A$, $O_B$, and $O_C$, respectively.
The lines $\ell_A$, $\ell_B$, $\ell_C$ perpendicular to $BC$, $CA$, and $AB$ pass through $O_A$, $O_B$, and $O_C$, respectively.
Prove that the circumcircle of triangle formed by $\ell_A$, $\ell_B$, and $\ell_C$ is tangent to the line $OP$.
 be the circumcentre, and
be the circumcentre, and  be the circumcircle of an acute-angled triangle
be the circumcircle of an acute-angled triangle  . Let
. Let  be an arbitrary point on
be an arbitrary point on  , distinct from
, distinct from  ,
,  ,
,  , and their antipodes in
, and their antipodes in  . Denote the circumcentres of the triangles
. Denote the circumcentres of the triangles 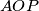 ,
, 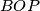 , and
, and 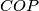 by
by 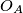 ,
, 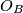 , and
, and 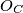 , respectively. The lines
, respectively. The lines 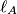 ,
, 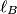 ,
, 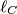 perpendicular to
perpendicular to  ,
,  , and
, and  pass through
pass through 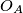 ,
, 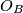 , and
, and 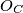 , respectively. Prove that the circumcircle of triangle formed by
, respectively. Prove that the circumcircle of triangle formed by 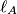 ,
, 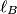 , and
, and 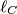 is tangent to the line
is tangent to the line 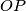 .
.  Školjka
Školjka