Let 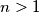 be a positive integer. Each cell of an
be a positive integer. Each cell of an 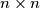 table contains an integer. Suppose that the following conditions are satisfied:
table contains an integer. Suppose that the following conditions are satisfied:
(i) Each number in the table is congruent to  modulo
modulo  ;
;
(ii) The sum of numbers in any row, as well as the sum of numbers in any column, is congruent to  modulo
modulo 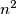 .
.
Let 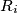 be the product of the numbers in the
be the product of the numbers in the 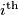 row, and
row, and 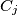 be the product of the number in the
be the product of the number in the 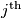 column. Prove that the sums
column. Prove that the sums 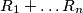 and
and 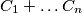 are congruent modulo
are congruent modulo 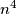 .
.
 Školjka
Školjka