Odredi sve funkcije 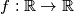 takve da jednakost
takve da jednakost 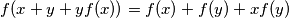 vrijedi za sve realne brojeve
vrijedi za sve realne brojeve 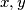 .
.
(Athanasios Kontogeorgis)
Odredi sve funkcije $f : \mathbb R \to \mathbb R$ takve da jednakost
$$ f(x+y+yf(x)) = f(x) + f(y) + xf(y) $$
vrijedi za sve realne brojeve $x,y$.
\begin{flushright}\emph{(Athanasios Kontogeorgis)}\end{flushright}