Neka su
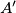
,
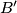
,
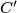
točke u kojima simetrale kutova trokuta

sijeku nasuprotne stranice

,

,

redom i neka je

središte upisane kružnice trokuta

.
Ako je
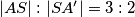
,
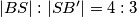
i ako je
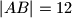
, odredi duljine ostalih stranica trokuta.
%V0
Neka su $A'$, $B'$, $C'$ točke u kojima simetrale kutova trokuta $ABC$ sijeku nasuprotne stranice $\overline{BC}$, $\overline{CA}$, $\overline{AB}$ redom i neka je $S$ središte upisane kružnice trokuta $ABC$.
Ako je $|AS| : |SA'| = 3 : 2$, $|BS| : |SB'| = 4 : 3$ i ako je $|AB|=12$, odredi duljine ostalih stranica trokuta.