Težište tetraedra

je točka

čiji je radijus-vektor dan sa
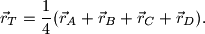
Ako je težište jednako udaljeno od vrhova

i

, dokažite da je
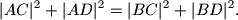
%V0
Težište tetraedra $ABCD$ je točka $T$ čiji je radijus-vektor dan sa $$
\displaystyle{\vec{r}_T=
\frac{1}{4}(\vec{r}_A+\vec{r}_B+\vec{r}_C+\vec{r}_D)}.
$$
Ako je težište jednako udaljeno od vrhova $A$ i $B$, dokažite da je $$
|AC|^2+|AD|^2=|BC|^2+|BD|^2.
$$