Teorem 1 (Homogena linearna diofantska jednadžba): Diofantska jednadžba oblika 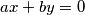 gdje su
gdje su 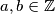 ,
, 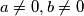 ima beskonačno mnogo cjelobrojnih rješenja, takvih da su
ima beskonačno mnogo cjelobrojnih rješenja, takvih da su 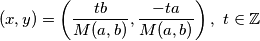
Teorem 2 (Linearna diofantska jednadžba): Diofantska jednadžba oblika 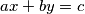 gdje su
gdje su 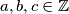 ,
, 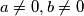 ima cjelobrojna rješenja ako i samo ako
ima cjelobrojna rješenja ako i samo ako 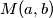 dijeli
dijeli  . Tada ih ima beskonačno mnogo. Također, sva su rješenja oblika zbroja jednog partikularnog i skupa rješenja homogenog.
. Tada ih ima beskonačno mnogo. Također, sva su rješenja oblika zbroja jednog partikularnog i skupa rješenja homogenog.
PRIMJER 1:
Riješimo homogenu diofantsku jednadžbu 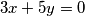 .
.
RJEŠENJE:
Izrazimo jednu nepoznanicu pomoću druge: 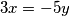 . Budući da je
. Budući da je  cijeli broj,
cijeli broj,  mora biti djeljiv s 3, tj.
mora biti djeljiv s 3, tj.  je oblika
je oblika 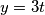 gdje je
gdje je  neki cijeli broj. Iz toga dobivamo da je
neki cijeli broj. Iz toga dobivamo da je 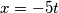 . Dobili smo da su rješenja početne jednadžbe svi uređeni parovi
. Dobili smo da su rješenja početne jednadžbe svi uređeni parovi 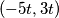 ,
, 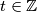 .
.
PRIMJER 2:
Riješimo diofantsku jednadžbu 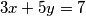 .
.
RJEŠENJE:
Pokušajmo pronaći neki par 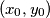 koji zadovoljava jednadžbu. Pogađanjem možemo naći uređen par
koji zadovoljava jednadžbu. Pogađanjem možemo naći uređen par 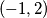 što nam je zapravo jedno partikularno rješenje naše diofantske jednadžbe.
što nam je zapravo jedno partikularno rješenje naše diofantske jednadžbe.
Promatrajmo sada homogenu jednadžbu 3x + 5y = 0. Iz prethodnog primjera znamo da su rješenja te jednadžbe svi uređeni parovi 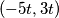 , gdje je
, gdje je 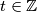 .
.
Iz Teorema 1.3. zaključujemo da su rješenja opće jednadžbe parovi 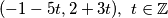 .
.
Zadatci za samostalno rješavanje
1. Riješi homogenu diofantsku jednadžbu: 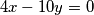 .
.
2. Riješi diofantsku jednadžbu: 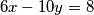 .
.
3. Riješi diofantsku jednadžbu: 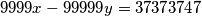 .
.
 Školjka
Školjka