Metoda posljednje znamenke je samo poseban slučaj metode kongruencija kojom ćemo se pozabaviti neki drugi put koristeći kao uvod predavanje s ovogodišnje Ljetne škole: https://drive.google.com/drive/folders/170lvUaNcIh_BsNTtRsrZHARXhKRW2-4t?usp=sharing
PRIMJER 1:
Riješi diofantsku jednadžbu 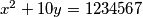 .
.
RJEŠENJE:
Kvadrat cijelog broja može završavati jednom od znamenaka 0, 1, 4, 5, 6 ili 9. S obzirom da 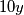 završava znamenkom 0, zadnja znamenka od
završava znamenkom 0, zadnja znamenka od 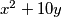 može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu 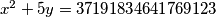 .
.
RJEŠENJE:
Budući da kvadrat cijelog broja završava sa znamenkom 0, 1, 4, 5, 6, ili 9,a broj 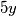 sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
Zadatci za samostalno rješavanje
1. Nađi sve parove prirodnih brojeva 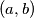 takvih da vrijedi:
takvih da vrijedi: 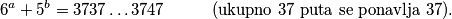
2. Nađite cjelobrojna rješenja jednadžbe: 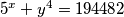 .
.
Metoda posljednje znamenke je samo poseban slučaj \textit{metode kongruencija} kojom ćemo se pozabaviti neki drugi put koristeći kao uvod predavanje s ovogodišnje Ljetne škole: \url{https://drive.google.com/drive/folders/170lvUaNcIh_BsNTtRsrZHARXhKRW2-4t?usp=sharing}
PRIMJER 1:
Riješi diofantsku jednadžbu $x^2 + 10y = 1234567$.
RJEŠENJE:
Kvadrat cijelog broja može završavati jednom od znamenaka 0, 1, 4, 5, 6 ili 9. S obzirom da $10y$ završava znamenkom 0, zadnja znamenka od $x^2+10y$ može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
PRIMJER 2:
Riješimo diofantsku jednadžbu $x^2 + 5y = 37191834641769123$.
RJEŠENJE:
Budući da kvadrat cijelog broja završava sa znamenkom 0, 1, 4, 5, 6, ili 9,a broj $5y$ sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
\textbf{Zadatci za samostalno rješavanje}
1. Nađi sve parove prirodnih brojeva $(a, b)$ takvih da vrijedi: $$6^a + 5^b = 3737 \dots 3747 \hspace{10mm} \text{(ukupno 37 puta se ponavlja 37).}$$
2. Nađite cjelobrojna rješenja jednadžbe: $5^x + y^4 = 194482$.
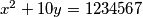 .
.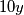 završava znamenkom 0, zadnja znamenka od
završava znamenkom 0, zadnja znamenka od 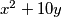 može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.
može biti 0, 1, 4, 5, 6 ili 9. Kako broj s desne strane jednakosti završava znamenkom 7, zadana jednadžba nema cjelobrojnih rješenja.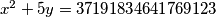 .
.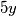 sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.
sa znamenkom 0 ili 5, slijedi da zbroj na lijevoj strani završava s 0, 1, 4, 5, 6, ili 9, a nikako s 3. Dakle, zadana diofantska jednadžba nema rješenja.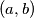 takvih da vrijedi:
takvih da vrijedi: 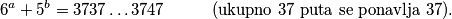
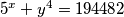 .
.  Školjka
Školjka