Na otoku živi  domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. Ogrlica može biti i bez kamenja. Dokažite da se poglavičina zapovijed može izvršiti koristeći najviše
domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. Ogrlica može biti i bez kamenja. Dokažite da se poglavičina zapovijed može izvršiti koristeći najviše 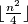 različitih vrsta kamenja.
različitih vrsta kamenja.
Na otoku živi $n$ domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. Ogrlica može biti i bez kamenja. Dokažite da se poglavičina zapovijed može izvršiti koristeći najviše $\lfloor \frac{n^2}{4} \rfloor$ različitih vrsta kamenja.
 domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. Ogrlica može biti i bez kamenja. Dokažite da se poglavičina zapovijed može izvršiti koristeći najviše
domorodaca. Svaka dva su ili prijatelji ili neprijatelji. Jednog dana poglavica naredi svim stanovnicima (uključujući i sebe) da si naprave i da nose kamene ogrlice, tako da svaka dva prijatelja imaju barem po jedan istovrsni kamen u svojim ogrlicama, a da se sva kamenja u ogrlicama dvaju neprijatelja razlikuju. Ogrlica može biti i bez kamenja. Dokažite da se poglavičina zapovijed može izvršiti koristeći najviše 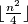 različitih vrsta kamenja.
različitih vrsta kamenja.  Školjka
Školjka