Neka je

točka unutar trostrane piramide

i neka su točke

,

,

,
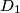
presjecišta pravaca
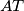
,
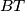
,
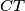
,
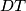
s nasuprotnim stranama piramide, redom. Ako je
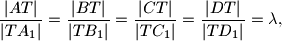
koje sve vrijednosti može
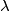
poprimiti? Obrazložite odgovor!
%V0
Neka je $T$ točka unutar trostrane piramide $ABCD$ i neka su točke $A_1$, $B_1$, $C_1$, $D_1$ presjecišta pravaca $AT$, $BT$, $CT$, $DT$ s nasuprotnim stranama piramide, redom. Ako je $$
\dfrac{|AT|}{|TA_1|}=\dfrac{|BT|}{|TB_1|}=\dfrac{|CT|}{|TC_1|}=
\dfrac{|DT|}{|TD_1|}=\lambda,
$$ koje sve vrijednosti može $\lambda$ poprimiti? Obrazložite odgovor!