Neka je
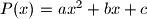
, gdje su

,

,
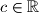
,
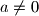
. Odredi sva rješenja jednadžbe
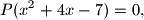
ako je poznato da je jedno od njih jednako

i barem jedno rješenje je dvostruko.
%V0
Neka je $P(x)=ax^2+bx+c$, gdje su $a$, $b$, $c\in \mathbb{R}$, $a\neq 0$. Odredi sva rješenja jednadžbe $$
P(x^2+4x-7)=0,
$$ ako je poznato da je jedno od njih jednako $1$ i barem jedno rješenje je dvostruko.