Neka su

,

i

stranice trokuta te

,

i

njima nasuprotni kutovi, redom. Dokaži da vrijedi
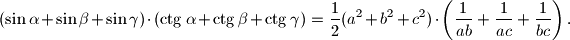
%V0
Neka su $a$, $b$ i $c$ stranice trokuta te $\alpha$, $\beta$ i $\gamma$ njima nasuprotni kutovi, redom. Dokaži da vrijedi $$
(\sin \alpha + \sin \beta + \sin \gamma ) \cdot
( \ctg \alpha + \ctg \beta + \ctg \gamma)\\
=\dfrac{1}{2} (a^2+b^2+c^2) \cdot
\left(\dfrac{1}{ab}+\dfrac{1}{ac}+\dfrac{1}{bc}\right).
$$