Školjka

%V0 Neka su $a$, $b$, $c$ pozitivni realni brojevi za koje vrijedi $a+b+c=abc$. Dokaži da vrijedi $$ a^5\left(bc-1\right)+b^5\left(ca-1\right)+c^5\left(ab-1\right)\ge 54\sqrt{3}. $$

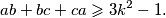
%V0 Dan je trokut $ABC$. Simetrala kuta $\angle CAB$ siječe stranicu $\overline{BC}$ u točki $D$, a simetrala kuta $\angle ABC$ siječe stranicu $\overline{AC}$ u točki $E$. Ako je $\angle ACB \ge 60^\circ$, dokaži da je $|AE|+|BD|\le |AB|$.

%V0 Odredi sve parove cijelih brojeva $(m, n)$ takvih da je $4 \cdot 3^{2m}+5=n^2$.

%V0 Odredite sve prirodne brojeve $n$ za koje je broj $$ 2^4+2^7+2^n $$ potpun kvadrat.

%V0 Neka su $n$ i $k$ prirodni brojevi. Dokažite da broj znamenaka u zapisu broja $5^n$ nije veći od $k$, ako i samo ako broj znamenaka u zapisu broja $2^n$ nije manji od $n-k+1$.

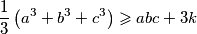
%V0 Neka su $a$, $b$, $c$ različiti prirodni brojevi i $k$ prirodan broj takav da vrijedi $$ \displaystyle ab + bc + ca \geqslant 3 k^2 -1 \text{.} $$ Dokaži da je $\displaystyle \frac13\left({a^3 + b^3 + c^3}\right) \geqslant abc + 3k$.