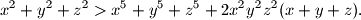Slični zadaci
Ivica mjeri svoju visinu na kraju svake školske godine. Do kraja osmog razreda osnovne škole visina je rasla kao aritmetički niz, a od tada kao geometrijski niz. Dokažite da Ivica u prvom razredu osnovne škole nije bio viši od 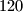 cm, ako je na kraju sedmog razreda imao
cm, ako je na kraju sedmog razreda imao 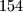 cm, na kraju prvog razreda srednje škole
cm, na kraju prvog razreda srednje škole 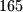 cm, a na kraju trećeg razreda srednje škole
cm, a na kraju trećeg razreda srednje škole 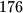 cm.
cm.
Napomena: Nije dozvoljeno koristiti kalkulator!
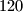 cm, ako je na kraju sedmog razreda imao
cm, ako je na kraju sedmog razreda imao 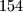 cm, na kraju prvog razreda srednje škole
cm, na kraju prvog razreda srednje škole 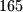 cm, a na kraju trećeg razreda srednje škole
cm, a na kraju trećeg razreda srednje škole 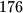 cm.
cm.Napomena: Nije dozvoljeno koristiti kalkulator!
 Školjka
Školjka  ,
,  ,
,  ,
,  članovi aritmetičkog i
članovi aritmetičkog i 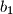 ,
, 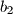 ,
, 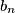 članovi geometrijskog niza s pozitivnim članovima. Ako je
članovi geometrijskog niza s pozitivnim članovima. Ako je 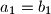 i
i 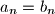 , dokažite da je suma članova aritmetičkog niza veća ili jednaka od sume članova geometrijskog niza.
, dokažite da je suma članova aritmetičkog niza veća ili jednaka od sume članova geometrijskog niza. 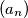 zadan je rekurzivno:
zadan je rekurzivno: 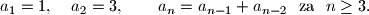 Dokaži da vrijedi nejednakost
Dokaži da vrijedi nejednakost 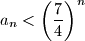 za sve
za sve  .
. 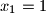 i
i 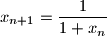 za svaki
za svaki 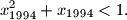
 vrijedi jednakost
vrijedi jednakost 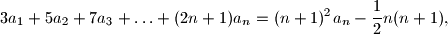 ako je
ako je 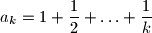 , za svaki prirodni broj
, za svaki prirodni broj  .
.  ,
,  ,
,  pozitivni realni brojevi za koje vrijedi
pozitivni realni brojevi za koje vrijedi 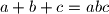 . Dokaži da vrijedi
. Dokaži da vrijedi 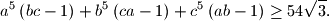
 ,
,  ,
,  pozitivni realni brojevi za koje vrijedi
pozitivni realni brojevi za koje vrijedi 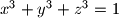 . Dokaži da je tada
. Dokaži da je tada