Na ploči  (
(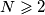 ) dva su dijagonalno suprotna kutna polja obojana u crno, a sva ostala obojana su u bijelo. U jednom koraku odaberemo redak ili stupac i promijenimo boju svakom polju u tom retku ili stupcu iz crne u bijelu i obratno. Koji je najmanji dodatni broj polja koje na početku moramo obojati u crno kako bismo nakon konačnog broja opisanih koraka mogli dobiti ploču na kojoj su sva polja crna?
) dva su dijagonalno suprotna kutna polja obojana u crno, a sva ostala obojana su u bijelo. U jednom koraku odaberemo redak ili stupac i promijenimo boju svakom polju u tom retku ili stupcu iz crne u bijelu i obratno. Koji je najmanji dodatni broj polja koje na početku moramo obojati u crno kako bismo nakon konačnog broja opisanih koraka mogli dobiti ploču na kojoj su sva polja crna?
Na ploči $N\times N$ ($N\geqslant 2$) dva su dijagonalno suprotna kutna polja obojana u crno, a sva ostala obojana su u bijelo. U jednom koraku odaberemo redak ili stupac i promijenimo boju svakom polju u tom retku ili stupcu iz crne u bijelu i obratno. Koji je najmanji dodatni broj polja koje na početku moramo obojati u crno kako bismo nakon konačnog broja opisanih koraka mogli dobiti ploču na kojoj su sva polja crna?
 (
(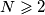 ) dva su dijagonalno suprotna kutna polja obojana u crno, a sva ostala obojana su u bijelo. U jednom koraku odaberemo redak ili stupac i promijenimo boju svakom polju u tom retku ili stupcu iz crne u bijelu i obratno. Koji je najmanji dodatni broj polja koje na početku moramo obojati u crno kako bismo nakon konačnog broja opisanih koraka mogli dobiti ploču na kojoj su sva polja crna?
) dva su dijagonalno suprotna kutna polja obojana u crno, a sva ostala obojana su u bijelo. U jednom koraku odaberemo redak ili stupac i promijenimo boju svakom polju u tom retku ili stupcu iz crne u bijelu i obratno. Koji je najmanji dodatni broj polja koje na početku moramo obojati u crno kako bismo nakon konačnog broja opisanih koraka mogli dobiti ploču na kojoj su sva polja crna?  Školjka
Školjka