Direktori dviju tvrtki nalaze se u točkama udaljenim 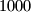 kilometara. U
kilometara. U  točaka na dužini između njih nalazi se po jedan matematičar. Svake sekunde u istom trenutku, svi matematičari se premještaju -- svaki ide na polovište dužine koja spaja njega i njemu najbližu osobu (matematičara ili direktora). Ako takva osoba nije jedinstvena, po volji bira jednu od njih. Ako na taj način dva matematičara dođu u istu točku, mlađi od njih zauvijek odlazi.
točaka na dužini između njih nalazi se po jedan matematičar. Svake sekunde u istom trenutku, svi matematičari se premještaju -- svaki ide na polovište dužine koja spaja njega i njemu najbližu osobu (matematičara ili direktora). Ako takva osoba nije jedinstvena, po volji bira jednu od njih. Ako na taj način dva matematičara dođu u istu točku, mlađi od njih zauvijek odlazi.
Dokaži da će se, nakon konačno mnogo sekundi, svaki od preostalih matematičara moći rukovati s jednim od direktora. Matematičar se može rukovati s direktorom ako je od njega udaljen za najviše  metar.
metar.
Direktori dviju tvrtki nalaze se u točkama udaljenim $1000$ kilometara. U $n$ točaka na dužini između njih nalazi se po jedan matematičar.
Svake sekunde u istom trenutku, svi matematičari se premještaju -- svaki ide na polovište dužine koja spaja njega i njemu najbližu osobu (matematičara ili direktora). Ako takva osoba nije jedinstvena, po volji bira jednu od njih. Ako na taj način dva matematičara dođu u istu točku, mlađi od njih zauvijek odlazi.
Dokaži da će se, nakon konačno mnogo sekundi, svaki od preostalih matematičara moći rukovati s jednim od direktora.
Matematičar se može rukovati s direktorom ako je od njega udaljen za najviše $1$ metar.
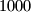 kilometara. U
kilometara. U  točaka na dužini između njih nalazi se po jedan matematičar. Svake sekunde u istom trenutku, svi matematičari se premještaju -- svaki ide na polovište dužine koja spaja njega i njemu najbližu osobu (matematičara ili direktora). Ako takva osoba nije jedinstvena, po volji bira jednu od njih. Ako na taj način dva matematičara dođu u istu točku, mlađi od njih zauvijek odlazi.
točaka na dužini između njih nalazi se po jedan matematičar. Svake sekunde u istom trenutku, svi matematičari se premještaju -- svaki ide na polovište dužine koja spaja njega i njemu najbližu osobu (matematičara ili direktora). Ako takva osoba nije jedinstvena, po volji bira jednu od njih. Ako na taj način dva matematičara dođu u istu točku, mlađi od njih zauvijek odlazi. metar.
metar.  Školjka
Školjka