Odredi sve funkcije 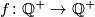 takve da vrijedi
takve da vrijedi 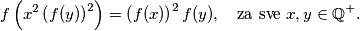
(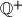 je oznaka za skup svih pozitivnih racionalnih brojeva.)
je oznaka za skup svih pozitivnih racionalnih brojeva.)
Odredi sve funkcije $f \colon \mathbb{Q}^+\to \mathbb{Q}^+$ takve da vrijedi
\[f\left(x^2\left(f(y)\right)^2\right) = \left(f(x)\right)^2f(y), \quad \text{za sve } x, y \in \mathbb{Q}^+\text.\]
($\mathbb{Q}^+$ je oznaka za skup svih pozitivnih racionalnih brojeva.)