Odredi sve funkcije 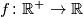 takve da vrijedi
takve da vrijedi 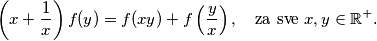
(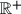 je oznaka za skup svih pozitivnih realnih brojeva.)
je oznaka za skup svih pozitivnih realnih brojeva.)
Odredi sve funkcije $f\colon \mathbb{R}^+\to \mathbb{R}$ takve da vrijedi
\[\left(x+\frac{1}{x}\right) f(y) = f(xy) + f\left(\frac{y}{x}\right), \quad \text{za sve } x, y \in \mathbb{R}^+\text.\]
($\mathbb{R}^+$ je oznaka za skup svih pozitivnih realnih brojeva.)