Let  ,
,  ,
,  be the midpoints of the arcs
be the midpoints of the arcs 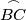 ,
, 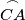 ,
, 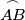 on the circumcircle of a triangle
on the circumcircle of a triangle  not containing the points
not containing the points  ,
,  ,
,  , respectively. Let the line
, respectively. Let the line 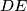 meets
meets  and
and  at
at  and
and  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 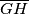 . Let the line
. Let the line 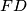 meet
meet  and
and  at
at  and
and 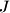 , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 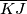 .
.
a) Find the angles of triangle 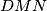 ;
;
b) Prove that if  is the point of intersection of the lines
is the point of intersection of the lines  and
and  , then the circumcenter of triangle
, then the circumcenter of triangle 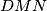 lies on the circumcircle of triangle
lies on the circumcircle of triangle 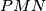 .
.
Let $D$, $E$, $F$ be the midpoints of the arcs $\overset{\frown}{BC}$, $\overset{\frown}{CA}$, $\overset{\frown}{AB}$ on the circumcircle of a triangle $ABC$ not containing the points $A$, $B$, $C$, respectively. Let the line $DE$ meets $BC$ and $CA$ at $G$ and $H$, and let $M$ be the midpoint of the segment $\overline{GH}$. Let the line $FD$ meet $BC$ and $AB$ at $K$ and $J$, and let $N$ be the midpoint of the segment $\overline{KJ}$.
a) Find the angles of triangle $DMN$;
b) Prove that if $P$ is the point of intersection of the lines $AD$ and $EF$, then the circumcenter of triangle $DMN$ lies on the circumcircle of triangle $PMN$.
 ,
,  ,
,  be the midpoints of the arcs
be the midpoints of the arcs 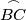 ,
, 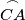 ,
, 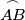 on the circumcircle of a triangle
on the circumcircle of a triangle  not containing the points
not containing the points  ,
,  ,
,  , respectively. Let the line
, respectively. Let the line 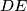 meets
meets  and
and  at
at  and
and  , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 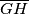 . Let the line
. Let the line 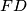 meet
meet  and
and  at
at  and
and 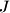 , and let
, and let  be the midpoint of the segment
be the midpoint of the segment 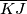 .
.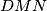 ;
; is the point of intersection of the lines
is the point of intersection of the lines  and
and  , then the circumcenter of triangle
, then the circumcenter of triangle 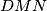 lies on the circumcircle of triangle
lies on the circumcircle of triangle 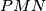 .
.  Školjka
Školjka