Dana je ploča dimenzija 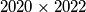 . Za dva polja te ploče kažemo da su susjedna ako imaju zajedničku stranicu ili se nalaze na početku i kraju istog retka ili stupca. Dakle, svako polje ima točno četiri susjedna polja.
. Za dva polja te ploče kažemo da su susjedna ako imaju zajedničku stranicu ili se nalaze na početku i kraju istog retka ili stupca. Dakle, svako polje ima točno četiri susjedna polja.
Viktor u svakom koraku bira jedno polje ploče i na ploču postavlja pet žetona: po jedan na odabrano polje i na svako polje susjedno odabranom. Nakon konačnog broja takvih koraka, na svakom polju nalazi se točno  žetona.
žetona.
Odredi najmanji mogući  .
.
Dana je ploča dimenzija $2020 \times 2022$.
Za dva polja te ploče kažemo da su \emph{susjedna} ako imaju zajedničku stranicu ili se nalaze na početku i kraju istog retka ili stupca. Dakle, svako polje ima točno četiri susjedna polja.
Viktor u svakom koraku bira jedno polje ploče i na ploču postavlja pet žetona: po jedan na odabrano polje i na svako polje susjedno odabranom.
Nakon konačnog broja takvih koraka, na svakom polju nalazi se točno $d$ žetona.
Odredi najmanji mogući $d$.
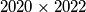 . Za dva polja te ploče kažemo da su susjedna ako imaju zajedničku stranicu ili se nalaze na početku i kraju istog retka ili stupca. Dakle, svako polje ima točno četiri susjedna polja.
. Za dva polja te ploče kažemo da su susjedna ako imaju zajedničku stranicu ili se nalaze na početku i kraju istog retka ili stupca. Dakle, svako polje ima točno četiri susjedna polja. žetona.
žetona. .
.  Školjka
Školjka