Dokaži da za sve realne brojeve 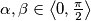 vrijedi
vrijedi 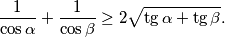 Kada vrijedi jednakost?
Kada vrijedi jednakost?
Dokaži da za sve realne brojeve $\alpha, \beta \in \left\langle 0, \frac{\pi}{2} \right\rangle$
vrijedi
\[ \frac{1}{\cos \alpha } + \frac{1}{\cos \beta } \geq 2\sqrt{\tg \alpha + \tg \beta}.\]
Kada vrijedi jednakost?