Ako su

,

i

realni brojevi za koje je
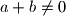
,
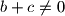
i
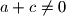
, dokaži da izraz:
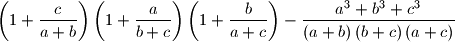
ne ovisi o vrijednostima brojeva

,

i

.
%V0
Ako su $a$, $b$ i $c$ realni brojevi za koje je $a+b\neq0$, $b+c\neq0$ i $a+c\neq0$, dokaži da izraz: $$
\left(1+\dfrac{c}{a+b}\right) \left( 1+\dfrac{a}{b+c}\right)
\left( 1+\dfrac{b}{a+c}\right) -\dfrac{a^{3}+b^{3}+c^{3}}
{\left(a+b\right) \left(b+c\right) \left(a+c\right)}
$$ ne ovisi o vrijednostima brojeva $a$, $b$ i $c$.