Neka je 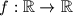 i neka vrijedi:
i neka vrijedi: 
Odredite sve realne brojeve  za koje takva funkcija postoji
za koje takva funkcija postoji
Neka je $f:\mathbb{R}\rightarrow\mathbb{R}$ i neka vrijedi:
\begin{enumerate}
\item $$f(f(x))=x,\quad\forall x\in\mathbb{R}$$
\item $f$ je neprekidna funkcija
\item postoji jedinstveni $a\in\mathbb{R}$ takav da je $$\lfloor f(a) \rfloor=\lfloor a \rfloor$$
\end{enumerate}
Odredite sve realne brojeve $a$ za koje takva funkcija postoji