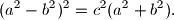Slični zadaci
Stranica  trokuta
trokuta  dira njegovu upisanu kružnicu u točki
dira njegovu upisanu kružnicu u točki  , a tom trokutu pripisana kružnica uz stranicu
, a tom trokutu pripisana kružnica uz stranicu  dira tu stranicu u točki
dira tu stranicu u točki  . Dokaži da su točke
. Dokaži da su točke  i
i  simetrične u odnosu na polovište stranice
simetrične u odnosu na polovište stranice  .
.
(Trokutu pripisana kružnica je kružnica koja dodiruje jednu stranicu trokuta i produžetke drugih dviju stranica.)
 trokuta
trokuta  dira njegovu upisanu kružnicu u točki
dira njegovu upisanu kružnicu u točki  , a tom trokutu pripisana kružnica uz stranicu
, a tom trokutu pripisana kružnica uz stranicu  dira tu stranicu u točki
dira tu stranicu u točki  . Dokaži da su točke
. Dokaži da su točke  i
i  simetrične u odnosu na polovište stranice
simetrične u odnosu na polovište stranice  .
.(Trokutu pripisana kružnica je kružnica koja dodiruje jednu stranicu trokuta i produžetke drugih dviju stranica.)
 Školjka
Školjka 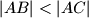 i neka je
i neka je 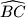 kružnice opisane tom trokutu na kojem leži točka
kružnice opisane tom trokutu na kojem leži točka  . Dokažite da za nožište
. Dokažite da za nožište  , vrijedi jednakost
, vrijedi jednakost 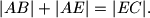
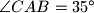 i
i 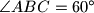 . Ako je
. Ako je  tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu
tangenta na kružnicu opisanu tom trokutu s diralištem u vrhu  , a
, a  paralela s pravcem
paralela s pravcem  kroz vrh
kroz vrh  cm, a duljina težišnice iz vrha pravog kuta
cm, a duljina težišnice iz vrha pravog kuta  cm. Odredi zbroj duljina kateta tog trokuta.
cm. Odredi zbroj duljina kateta tog trokuta. 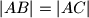 ) a točka
) a točka  i okomice iz vrha
i okomice iz vrha 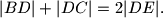
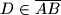 i
i 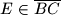 takve da je
takve da je 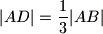 i
i 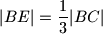 . Pravci
. Pravci  i
i  . Koliki je kut
. Koliki je kut 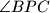 ?
? 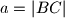 ,
, 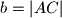 ,
, 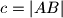 opisana je kružnica. Tangenta na tu kružnicu u točki
opisana je kružnica. Tangenta na tu kružnicu u točki  . Dokažite da je
. Dokažite da je