Riješite sustav jednadžbi:
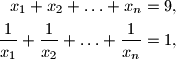
gdje je

prirodan broj, a

,
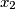
,

,
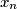
su pozitivni realni brojevi.
%V0
Riješite sustav jednadžbi: $$$\begin{align*}
x_1+x_2+\ldots +x_n &= 9, \\
\displaystyle{\dfrac{1}{x_1}+\dfrac{1}{x_2}+\ldots +\dfrac{1}{x_n}}&=1,
\end{align*}$$$ gdje je $n$ prirodan broj, a $x_1$, $x_2$, $\dots$, $x_n$ su pozitivni realni brojevi.