Trokut

je jednakokračan (
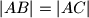
) a točka

je na onom luku
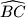
trokutu opisane kružnice koji ne sadrži vrh

. Nadalje, točka

je sjecište pravca

i okomice iz vrha

na taj pravac. Dokažite da vrijedi:
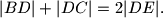
%V0
Trokut $ABC$ je jednakokračan ($|AB|=|AC|$) a točka $D$ je na onom luku $\widehat{BC}$ trokutu opisane kružnice koji ne sadrži vrh $A$. Nadalje, točka $E$ je sjecište pravca $CD$ i okomice iz vrha $A$ na taj pravac. Dokažite da vrijedi: $$|BD|+|DC|=2|DE|.$$