U skupu realnih brojeva riješite jednadžbu
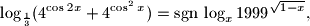
pri čemu je
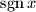
jednak

za
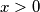
,

za
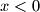
i

za
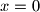
.
%V0
U skupu realnih brojeva riješite jednadžbu $$
\log_{\frac13}(4^{\cos{2x}}+4^{\cos^2x}) = \mathrm{sgn} \, \log_x 1999^{\sqrt{1-x}},
$$ pri čemu je $\mathrm{sgn} \, x$ jednak $1$ za $x > 0$, $-1$ za $x < 0$ i $0$ za $x = 0$.