Točno
16. travnja 2012. 18:11 (13 godine, 9 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
prva stvar: dokazati da 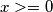
pretpostavimo da je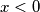
neka je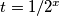
tada je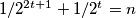 ,
, 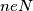
odnosno
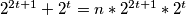
lijeva strana daje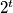 pri djeljenu s brojem
pri djeljenu s brojem 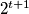 , dok desna strana daje
, dok desna strana daje 
zbog toga ne postoji nti jedno rješenje jednadžbe ako je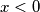
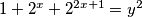
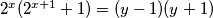
ako nađem rješenja za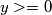 , tada sam pronašao i rješenja za
, tada sam pronašao i rješenja za 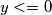
pretpostavimo da je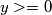
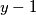 i
i 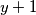 su 2 uzastopna parna prirodna broja, te je zato jedan djeljiv s
su 2 uzastopna parna prirodna broja, te je zato jedan djeljiv s  , a drugi s
, a drugi s 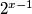
postoje 2 slučaja:
1)
1/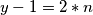
2/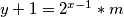
ako pišemo umjesto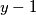 broj
broj 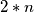 i umjesto
i umjesto 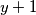 broj
broj 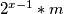 , množenjem se dobiva:
, množenjem se dobiva:
3/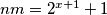
1/ - 2/ --->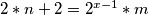
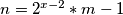
ako u 3/ umjesto n pišem gore navedeni izraz:
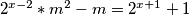
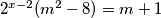
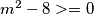
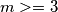
ako je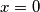 jednadžba nema rješenja
jednadžba nema rješenja
ako je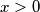 , tada je
, tada je 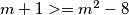
jedino rješenje je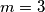 , zbog brzog rasta
, zbog brzog rasta 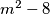
za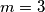 se dobiva
se dobiva 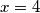 ,
, 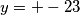
2)
1/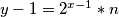
2/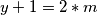
ako pišemo umjesto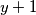 broj
broj 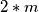 i umjesto
i umjesto 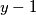 broj
broj 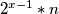 , množenjem se dobiva
, množenjem se dobiva
3/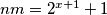
1/ - 2/ -->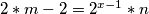
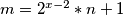
u jednakost 3/ umjesto m pišem gore navedeni izraz:
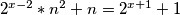
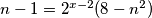
za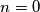 je lijeva strana negativna, a desna pozitivna
je lijeva strana negativna, a desna pozitivna
za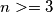 je desna strana negativna, a lijeva pozitivna
je desna strana negativna, a lijeva pozitivna
za nema rješenja
nema rješenja
za je rješenje
je rješenje 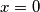 ,
, 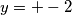
zaključujem da su rješenja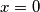 ,
, 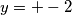 i
i 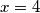 ,
, 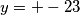
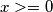
pretpostavimo da je
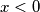
neka je
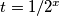
tada je
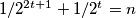 ,
, 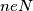
odnosno
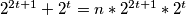
lijeva strana daje
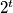 pri djeljenu s brojem
pri djeljenu s brojem 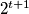 , dok desna strana daje
, dok desna strana daje 
zbog toga ne postoji nti jedno rješenje jednadžbe ako je
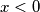
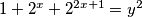
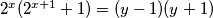
ako nađem rješenja za
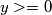 , tada sam pronašao i rješenja za
, tada sam pronašao i rješenja za 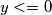
pretpostavimo da je
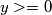
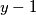 i
i 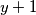 su 2 uzastopna parna prirodna broja, te je zato jedan djeljiv s
su 2 uzastopna parna prirodna broja, te je zato jedan djeljiv s  , a drugi s
, a drugi s 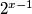
postoje 2 slučaja:
1)
1/
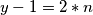
2/
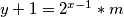
ako pišemo umjesto
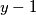 broj
broj 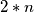 i umjesto
i umjesto 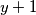 broj
broj 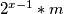 , množenjem se dobiva:
, množenjem se dobiva:3/
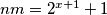
1/ - 2/ --->
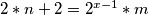
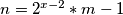
ako u 3/ umjesto n pišem gore navedeni izraz:
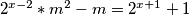
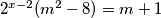
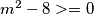
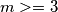
ako je
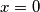 jednadžba nema rješenja
jednadžba nema rješenjaako je
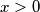 , tada je
, tada je 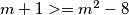
jedino rješenje je
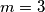 , zbog brzog rasta
, zbog brzog rasta 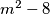
za
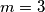 se dobiva
se dobiva 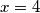 ,
, 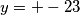
2)
1/
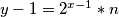
2/
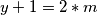
ako pišemo umjesto
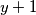 broj
broj 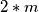 i umjesto
i umjesto 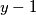 broj
broj 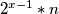 , množenjem se dobiva
, množenjem se dobiva3/
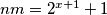
1/ - 2/ -->
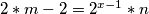
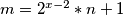
u jednakost 3/ umjesto m pišem gore navedeni izraz:
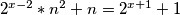
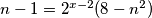
za
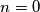 je lijeva strana negativna, a desna pozitivna
je lijeva strana negativna, a desna pozitivnaza
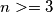 je desna strana negativna, a lijeva pozitivna
je desna strana negativna, a lijeva pozitivnaza
 nema rješenja
nema rješenjaza
 je rješenje
je rješenje 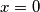 ,
, 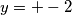
zaključujem da su rješenja
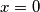 ,
, 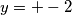 i
i 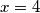 ,
, 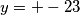
 Školjka
Školjka 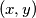 of integers such that
of integers such that