 be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let  be the incircle of triangle
be the incircle of triangle  . The median
. The median  of triangle
of triangle  intersects the incircle
intersects the incircle  at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle  again in two points
again in two points  and
and  . Let the lines
. Let the lines 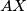 and
and 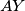 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 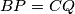 .
. Kliknite ovdje kako biste prikazali rješenje.
Uvedimo 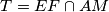 ,
,  kao presjek tangenti na
kao presjek tangenti na  u tockama
u tockama  i
i  te
te  kao presliku
kao presliku  preko
preko  .
. 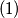
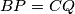
 ,
, ,
, kolinearne jer tada postoji homotetija sa centrom
kolinearne jer tada postoji homotetija sa centrom  koja salje
koja salje  ,
,  i
i  u
u  ,
,  i
i  redom.
redom. 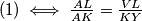 jer
jer 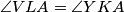 .
.
Buduci da se tangente na  u tockama
u tockama  i
i  sijeku na pravcu
sijeku na pravcu 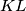 slijedi da je cetverokut
slijedi da je cetverokut 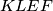 harmonicni tj.
harmonicni tj. 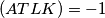
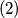 . Uocimo dalje da je
. Uocimo dalje da je 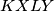 jednakokracni trapez pa mu je sjeciste dijagonala na simetrali osnovica to jest
jednakokracni trapez pa mu je sjeciste dijagonala na simetrali osnovica to jest  lezi na
lezi na 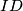 .
.
Lemma 1 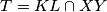 tvrdnju dokazujemo baricentricnim koordinatama, vrijedi
tvrdnju dokazujemo baricentricnim koordinatama, vrijedi 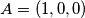 ,
, 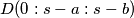 ,
, 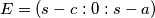 ,
, 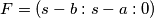 ,
, 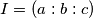 i
i 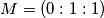 pa dobivamo
pa dobivamo 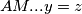 odakle mozemo pisati
odakle mozemo pisati 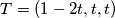 pa zbog
pa zbog  ,
,  ,
,  kolinearne imamo
kolinearne imamo 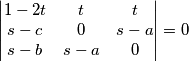 .
.
Odakle slijedi 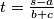 sto daje
sto daje 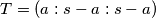 pa
pa 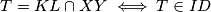 pa je nuzno i dovoljno pokazati
pa je nuzno i dovoljno pokazati 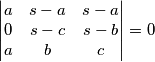 .
.
Zbrajanjem drugog reda prvom i oduzimanjem treceg se lako vidi da je dana matrica jednaka 0.
Alternativni dokaz Lemme 1  . Cetverokut
. Cetverokut 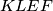 harmonicni pa vrijedi
harmonicni pa vrijedi  pa slijedi da je
pa slijedi da je  tocka u beskonacnosti jer je
tocka u beskonacnosti jer je  poloviste
poloviste  . Neka je
. Neka je 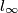 pravac u beskonacnosti.
pravac u beskonacnosti. 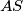 i
i  su redom polare od
su redom polare od  i
i  u odnosu na
u odnosu na 
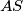 ,
,  ,
,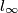 konkurentni
konkurentni 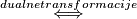
 ,
,  ,
,  -kolinearne cime smo dokazali Lemmu1
-kolinearne cime smo dokazali Lemmu1
Sada vrijedi 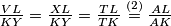 pa vrijedi i
pa vrijedi i 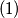 cime smo gotovi.
cime smo gotovi.
 Školjka
Školjka