IMO Shortlist 2005 problem G6
Kvaliteta:
Avg: 0,0Težina:
Avg: 8,0 Let  be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let 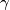 be the incircle of triangle
be the incircle of triangle  . The median
. The median 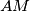 of triangle
of triangle  intersects the incircle
intersects the incircle 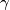 at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle 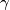 again in two points
again in two points  and
and 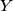 . Let the lines
. Let the lines 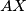 and
and 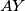 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 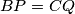 .
.
 be a triangle, and
be a triangle, and  the midpoint of its side
the midpoint of its side  . Let
. Let 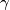 be the incircle of triangle
be the incircle of triangle  . The median
. The median 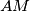 of triangle
of triangle  intersects the incircle
intersects the incircle 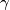 at two points
at two points  and
and  . Let the lines passing through
. Let the lines passing through  and
and  , parallel to
, parallel to  , intersect the incircle
, intersect the incircle 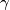 again in two points
again in two points  and
and 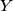 . Let the lines
. Let the lines 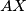 and
and 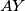 intersect
intersect  again at the points
again at the points  and
and  . Prove that
. Prove that 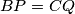 .
. Izvor: Međunarodna matematička olimpijada, shortlist 2005
 Školjka
Školjka 
