Točno
12. kolovoza 2017. 02:32 (8 godine, 7 mjeseci)
Dan je šiljastokutni trokut $ABC$ s visinama $\overline{AD}$, $\overline{BE}$ i $\overline{CF}$ te ortocentrom $H$. Dužine
$\overline{EF}$ i $\overline{AD}$ sijeku se u točki $G$. Dužina $\overline{AK}$ je promjer kružnice opisane trokutu $ABC$ i
siječe stranicu $\overline{BC}$ u točki $M$. Dokaži da su pravci $GM$ i $HK$ paralelni.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Lemma 1
Neka je  ortocentar trokuta
ortocentar trokuta  i neka je
i neka je  njegova opisana kružnica. Neka je
njegova opisana kružnica. Neka je  polovište stranice
polovište stranice  . Ako je
. Ako je  preslika točke
preslika točke  preko točke
preko točke  , onda
, onda  leži na kružnici
leži na kružnici  te je
te je 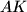 promjer te kružnice.
promjer te kružnice.
Dokaz: Neka se točke nalaze u kompleksnoj ravnini te neka je  ishodište navedene. Poznato je da je
ishodište navedene. Poznato je da je  =
= 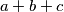 te
te 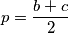 . S obzirom da je
. S obzirom da je 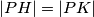 ,
, 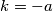 što direktno implicira da se točka nalazi na kružnici te da je
što direktno implicira da se točka nalazi na kružnici te da je 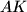 promjer kružnice.
promjer kružnice.
Lemma 2
Ako su  i
i  nožišta visina iz
nožišta visina iz  i
i  redom te ako je
redom te ako je  pravac tangentan na opisanu kružnicu trokuta
pravac tangentan na opisanu kružnicu trokuta  u točki A, onda je
u točki A, onda je 

 .
.
Dokaz: Neka je 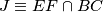 . Četverokut
. Četverokut 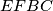 je tetivan te vrijedi da je
je tetivan te vrijedi da je 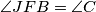 . Po poučku o kutu između tangente i tetive vrijedi
. Po poučku o kutu između tangente i tetive vrijedi 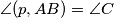 odakle slijedi
odakle slijedi 

 .
.
Neka je  polovište stranice
polovište stranice  te neka je
te neka je 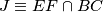 . Uočimo da je točka
. Uočimo da je točka  središte tetivnog četverokuta
središte tetivnog četverokuta 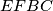 . Primjenom Brokardovog teorema na četverokut
. Primjenom Brokardovog teorema na četverokut 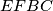 , dobivamo da je
, dobivamo da je 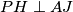 , a kako su
, a kako su  ,
,  i
i  kolinearne, vrijedi da je
kolinearne, vrijedi da je 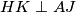 . Preostaje još pokazati da je
. Preostaje još pokazati da je 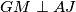 . Promotrimo trokut
. Promotrimo trokut 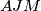 . U njemu imamo da je
. U njemu imamo da je 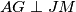 te vrijedi da je
te vrijedi da je 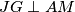 jer je
jer je 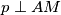 , a također vrijedi
, a također vrijedi 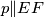 . Iz navedenog, možemo zaključiti da je
. Iz navedenog, možemo zaključiti da je  ortocentar trokuta
ortocentar trokuta 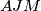 te vrijedi da je
te vrijedi da je 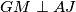 . Kako je
. Kako je 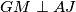 te
te 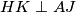 , vrijedi
, vrijedi 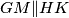 što je trebalo i dokazati.
što je trebalo i dokazati.
\textbf{Lemma 1}\\
Neka je $H$ ortocentar trokuta $ABC$ i neka je $\omega$ njegova opisana kružnica. Neka je $P$ polovište stranice $BC$. Ako je $K$ preslika točke $H$ preko točke $P$, onda $K$ leži na kružnici $\omega$ te je $AK$ promjer te kružnice.\\ \\
\emph{Dokaz}: Neka se točke nalaze u kompleksnoj ravnini te neka je $O$ ishodište navedene. Poznato je da je $h$ = $a+b+c$ te $p = \dfrac{b+c}{2}$. S obzirom da je $|PH| = |PK|$, $k = -a$ što direktno implicira da se točka nalazi na kružnici te da je $AK$ promjer kružnice.\\ \\
\textbf{Lemma 2}\\
Ako su $E$ i $F$ nožišta visina iz $B$ i $C$ redom te ako je $p$ pravac tangentan na opisanu kružnicu trokuta $ABC$ u točki A, onda je $p$ $ \|$ $EF$.
\emph{Dokaz}: Neka je $J \equiv EF \cap BC$. Četverokut $EFBC$ je tetivan te vrijedi da je $\angle JFB = \angle C$. Po poučku o kutu između tangente i tetive vrijedi $\angle (p,AB) = \angle C$ odakle slijedi $p$ $ \|$ $EF$. \\
\\
\\
Neka je $P$ polovište stranice $BC$ te neka je $J \equiv EF \cap BC$. Uočimo da je točka $P$ središte tetivnog četverokuta $EFBC$. Primjenom Brokardovog teorema na četverokut $EFBC$, dobivamo da je $PH \perp AJ$, a kako su $P$, $H$ i $K$ kolinearne, vrijedi da je $HK \perp AJ$. Preostaje još pokazati da je $GM \perp AJ$. Promotrimo trokut $AJM$. U njemu imamo da je $AG \perp JM$ te vrijedi da je $JG \perp AM$ jer je $p \perp AM$, a također vrijedi $p \| EF$. Iz navedenog, možemo zaključiti da je $G$ ortocentar trokuta $AJM$ te vrijedi da je $GM \perp AJ$. Kako je $GM \perp AJ$ te $HK \perp AJ$, vrijedi $GM \| HK$ što je trebalo i dokazati.
| 12. kolovoza 2017. 10:57 | abeker | Točno |
| 12. kolovoza 2017. 16:57 | krsto | Točno |
 ortocentar trokuta
ortocentar trokuta  i neka je
i neka je  njegova opisana kružnica. Neka je
njegova opisana kružnica. Neka je  polovište stranice
polovište stranice  . Ako je
. Ako je  preslika točke
preslika točke  preko točke
preko točke  , onda
, onda  leži na kružnici
leži na kružnici  te je
te je 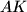 promjer te kružnice.
promjer te kružnice. ishodište navedene. Poznato je da je
ishodište navedene. Poznato je da je  =
= 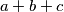 te
te 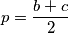 . S obzirom da je
. S obzirom da je 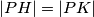 ,
, 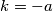 što direktno implicira da se točka nalazi na kružnici te da je
što direktno implicira da se točka nalazi na kružnici te da je 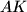 promjer kružnice.
promjer kružnice. i
i  nožišta visina iz
nožišta visina iz  i
i  redom te ako je
redom te ako je  pravac tangentan na opisanu kružnicu trokuta
pravac tangentan na opisanu kružnicu trokuta  u točki A, onda je
u točki A, onda je 

 .
.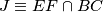 . Četverokut
. Četverokut 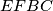 je tetivan te vrijedi da je
je tetivan te vrijedi da je 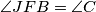 . Po poučku o kutu između tangente i tetive vrijedi
. Po poučku o kutu između tangente i tetive vrijedi 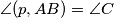 odakle slijedi
odakle slijedi 

 .
.  polovište stranice
polovište stranice  te neka je
te neka je 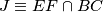 . Uočimo da je točka
. Uočimo da je točka  središte tetivnog četverokuta
središte tetivnog četverokuta 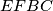 . Primjenom Brokardovog teorema na četverokut
. Primjenom Brokardovog teorema na četverokut 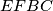 , dobivamo da je
, dobivamo da je 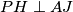 , a kako su
, a kako su  ,
,  i
i  kolinearne, vrijedi da je
kolinearne, vrijedi da je 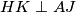 . Preostaje još pokazati da je
. Preostaje još pokazati da je 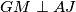 . Promotrimo trokut
. Promotrimo trokut 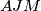 . U njemu imamo da je
. U njemu imamo da je 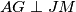 te vrijedi da je
te vrijedi da je 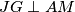 jer je
jer je 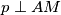 , a također vrijedi
, a također vrijedi 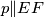 . Iz navedenog, možemo zaključiti da je
. Iz navedenog, možemo zaključiti da je  ortocentar trokuta
ortocentar trokuta 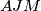 te vrijedi da je
te vrijedi da je 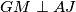 . Kako je
. Kako je 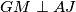 te
te 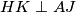 , vrijedi
, vrijedi 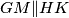 što je trebalo i dokazati.
što je trebalo i dokazati.  Školjka
Školjka 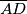 ,
, 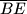 i
i 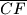 te ortocentrom
te ortocentrom 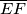 i
i 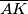 je promjer kružnice opisane trokutu
je promjer kružnice opisane trokutu  u točki
u točki  . Dokaži da su pravci
. Dokaži da su pravci 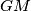 i
i 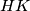 paralelni.
paralelni.