Tvrdnju cemo dokazati baricentricnim koordinatama uz preliku ravnive tako da je  ishodiste ravnine i neku su
ishodiste ravnine i neku su  ,
, i
i  stranice trokuta
stranice trokuta  , vrijedi
, vrijedi 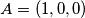 ,
, 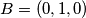 ,
, 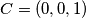 i
i 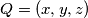 a buduci da je
a buduci da je  na paraleli sa
na paraleli sa  kroz
kroz  i
i  na
na  slijedi
slijedi 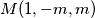 i
i 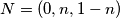 . Koristeci pseudo vektor
. Koristeci pseudo vektor 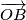 i kriterij okomitosti
i kriterij okomitosti 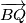 i
i 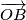 slijedi da je jednadzba pravca
slijedi da je jednadzba pravca 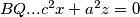 . Analogno se dobiva
. Analogno se dobiva 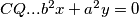 odakle se vidi da je jedno rjesenje sustava
odakle se vidi da je jedno rjesenje sustava 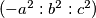 pa dobivamo
pa dobivamo 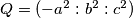 , s obzirom da su
, s obzirom da su  ,
, ,
, kolinearne mora vrijediti
kolinearne mora vrijediti 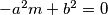 odakle slijedi
odakle slijedi 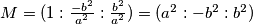 pravac
pravac 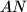 zadan je sa
zadan je sa 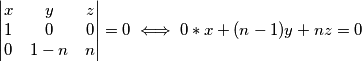 pa buduci da
pa buduci da 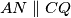 vrijedi
vrijedi 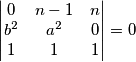 iz cega slijnedi
iz cega slijnedi 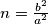 pa dobivamo
pa dobivamo 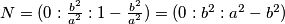 . Sada buduci da se
. Sada buduci da se  nalazi na
nalazi na 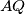 mozemo staviti
mozemo staviti 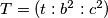 za neki realan broj
za neki realan broj  . Zbog kolinearnosti
. Zbog kolinearnosti  ,
, ,
, slijedi
slijedi 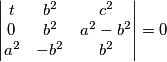 pa rjesavanjem jednadzbe po
pa rjesavanjem jednadzbe po  se dobiva
se dobiva 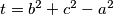 slijedi
slijedi 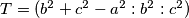 . Oznacimo
. Oznacimo 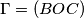 pa prema jednadzbi za kruznicu u baricentricnim koordinatama imamo
pa prema jednadzbi za kruznicu u baricentricnim koordinatama imamo 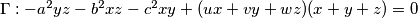 za neke realne konstante
za neke realne konstante  ,
, i
i  pa uvrstavanjem
pa uvrstavanjem  ,
, i
i  u
u  dobivamo redom
dobivamo redom 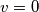 ,
, 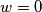 i
i 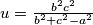 pa konacno imamo
pa konacno imamo 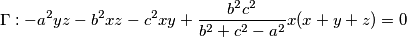 Uvrstimo sada
Uvrstimo sada  u
u  , imamo
, imamo 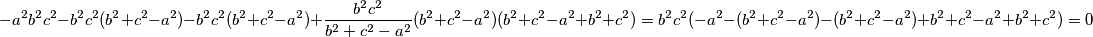 pa
pa 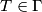 .
.
Tvrdnju cemo dokazati baricentricnim koordinatama uz preliku ravnive tako da je $O$ ishodiste ravnine i neku su $a$,$b$ i $c$ stranice trokuta $ABC$, vrijedi $A=(1,0,0)$ , $B=(0,1,0)$ , $C=(0,0,1)$ i $Q=(x,y,z)$ a buduci da je $M$ na paraleli sa $BC$ kroz $A$ i $N$ na $BC$ slijedi $M(1,-m,m)$ i $N=(0,n,1-n) $.
Koristeci pseudo vektor $\overrightarrow{OB}$ i kriterij okomitosti $\overrightarrow{BQ}$ i $\overrightarrow{OB}$ slijedi da je jednadzba pravca $BQ ...c^2x+a^2z=0$ . Analogno se dobiva $CQ... b^2x+a^2y=0$ odakle se vidi da je jedno rjesenje sustava $(-a^2:b^2:c^2)$ pa dobivamo $Q=(-a^2:b^2:c^2)$, s obzirom da su $M$,$C$,$Q$ kolinearne mora vrijediti $-a^2m+b^2=0$ odakle slijedi $M=(1:\frac{-b^2}{a^2}:\frac{b^2}{a^2}) =(a^2:-b^2:b^2)$ pravac $AN$ zadan je sa $\begin{vmatrix}x & y & z \\1 & 0 & 0 \\0 & 1-n & n \end{vmatrix}=0 \iff 0*x+(n-1)y+nz=0$ pa buduci da $AN \parallel CQ$ vrijedi $\begin{vmatrix}0 & n-1 & n \\b^2 & a^2 & 0 \\1 & 1 & 1 \end{vmatrix}=0$ iz cega slijnedi $n=\frac{b^2}{a^2}$ pa dobivamo $N=(0:\frac{b^2}{a^2}:1-\frac{b^2}{a^2})=(0:b^2:a^2-b^2)$. Sada buduci da se $T$ nalazi na $AQ$ mozemo staviti $T=(t:b^2:c^2)$ za neki realan broj $t$. Zbog kolinearnosti $N$,$T$,$M$ slijedi $\begin{vmatrix}t & b^2 & c^2 \\0 & b^2 & a^2-b^2 \\a^2 & -b^2 & b^2 \end{vmatrix}=0$ pa rjesavanjem jednadzbe po $t$ se dobiva $t=b^2+c^2-a^2$ slijedi $T=(b^2+c^2-a^2:b^2:c^2)$. Oznacimo $\Gamma=(BOC)$ pa prema jednadzbi za kruznicu u baricentricnim koordinatama imamo $\Gamma : -a^2yz-b^2xz-c^2xy+(ux+vy+wz)(x+y+z)=0$ za neke realne konstante $u$,$v$ i $w$ pa uvrstavanjem $B$,$C$ i $Q$ u $\Gamma$ dobivamo redom $v=0$ , $w=0$ i $u=\frac{b^2c^2}{b^2+c^2-a^2}$ pa konacno imamo $$\Gamma : -a^2yz-b^2xz-c^2xy+\frac{b^2c^2}{b^2+c^2-a^2}x(x+y+z)=0$$
Uvrstimo sada $T$ u $\Gamma$, imamo
$$ -a^2b^2c^2-b^2c^2(b^2+c^2-a^2)-b^2c^2(b^2+c^2-a^2)+\frac{b^2c^2}{b^2+c^2-a^2}(b^2+c^2-a^2)(b^2+c^2-a^2+b^2+c^2)
=b^2c^2(-a^2-(b^2+c^2-a^2)-(b^2+c^2-a^2)+b^2+c^2-a^2+b^2+c^2)=0$$ pa $T \in \Gamma$.
 u kojem vrijedi
u kojem vrijedi 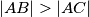 . Neka je
. Neka je  središte kružnice opisane tom trokutu, a
središte kružnice opisane tom trokutu, a 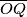 promjer kružnice opisane trokutu
promjer kružnice opisane trokutu 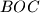 . Pravac paralelan s pravcem
. Pravac paralelan s pravcem  kroz
kroz  siječe pravac
siječe pravac 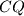 u točki
u točki  , a pravac paralelan s pravcem
, a pravac paralelan s pravcem 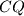 kroz
kroz  siječe pravac
siječe pravac  u točki
u točki  . Neka je
. Neka je  presjek pravaca
presjek pravaca 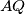 i
i  . Dokaži da točka
. Dokaži da točka  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu 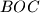 .
.  ishodiste ravnine i neku su
ishodiste ravnine i neku su  ,
, i
i  stranice trokuta
stranice trokuta  , vrijedi
, vrijedi 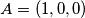 ,
, 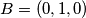 ,
, 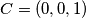 i
i 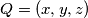 a buduci da je
a buduci da je  na paraleli sa
na paraleli sa  kroz
kroz  i
i  na
na  slijedi
slijedi 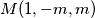 i
i 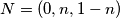 . Koristeci pseudo vektor
. Koristeci pseudo vektor 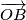 i kriterij okomitosti
i kriterij okomitosti 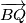 i
i 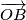 slijedi da je jednadzba pravca
slijedi da je jednadzba pravca 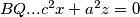 . Analogno se dobiva
. Analogno se dobiva 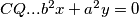 odakle se vidi da je jedno rjesenje sustava
odakle se vidi da je jedno rjesenje sustava 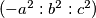 pa dobivamo
pa dobivamo 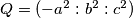 , s obzirom da su
, s obzirom da su  ,
, ,
, kolinearne mora vrijediti
kolinearne mora vrijediti 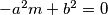 odakle slijedi
odakle slijedi 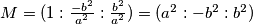 pravac
pravac 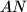 zadan je sa
zadan je sa 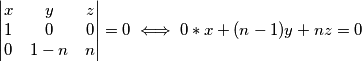 pa buduci da
pa buduci da 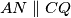 vrijedi
vrijedi 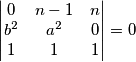 iz cega slijnedi
iz cega slijnedi 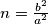 pa dobivamo
pa dobivamo 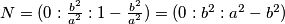 . Sada buduci da se
. Sada buduci da se  nalazi na
nalazi na 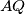 mozemo staviti
mozemo staviti 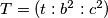 za neki realan broj
za neki realan broj  . Zbog kolinearnosti
. Zbog kolinearnosti  ,
, ,
, slijedi
slijedi 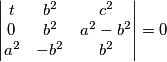 pa rjesavanjem jednadzbe po
pa rjesavanjem jednadzbe po  se dobiva
se dobiva 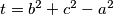 slijedi
slijedi 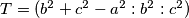 . Oznacimo
. Oznacimo 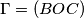 pa prema jednadzbi za kruznicu u baricentricnim koordinatama imamo
pa prema jednadzbi za kruznicu u baricentricnim koordinatama imamo 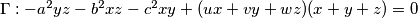 za neke realne konstante
za neke realne konstante  ,
, i
i  pa uvrstavanjem
pa uvrstavanjem  ,
, i
i  u
u  dobivamo redom
dobivamo redom 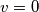 ,
, 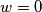 i
i 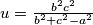 pa konacno imamo
pa konacno imamo 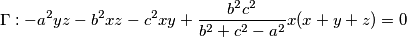 Uvrstimo sada
Uvrstimo sada  u
u  , imamo
, imamo 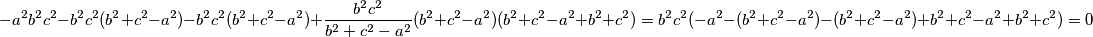 pa
pa 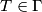 .
.  Školjka
Školjka