Neocijenjeno
6. studenoga 2017. 23:13 (8 godine, 3 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Pretpostavimo da za neki prost broj  postoje cijeli brojevi
postoje cijeli brojevi 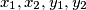 takvi da skupovi
takvi da skupovi 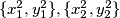 nisu jednaki i:
nisu jednaki i: 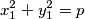
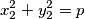
Odmah mozemo provjeriti da za 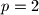 ne postoje takvi brojevi. Takoder
ne postoje takvi brojevi. Takoder 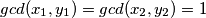
Iz cinjenice da je  suma kvadrata slijedi da
suma kvadrata slijedi da  mora biti oblika
mora biti oblika  mod 4.
mod 4.
Tada 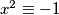 mod
mod  ima tocno dva rjesenja,
ima tocno dva rjesenja,  i
i 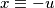 za neki prirodan
za neki prirodan  .
.
(Konkretnije 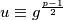 gdje je
gdje je 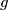 primitivni korijen modulo
primitivni korijen modulo  )
)
Dakle 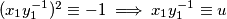 , Predpostavimo pozitivan predznak od
, Predpostavimo pozitivan predznak od  jer uvijek mozemo transformirati
jer uvijek mozemo transformirati  u
u 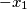 .
.
Analogno 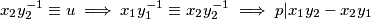
Ovo postaje korisno jer 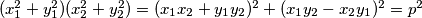
Tada 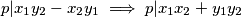
Ako vrijedi: 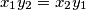 , zato sto
, zato sto 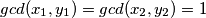 tada
tada 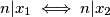 , te
, te 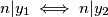
Sad znamo da  i
i 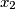 imaju istu faktorizaciju dakle
imaju istu faktorizaciju dakle 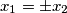 i analogno
i analogno 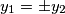 .
. 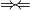
Slicno mozemo reci i u slucaju 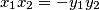 , tada je
, tada je 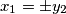 i
i 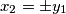
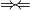
Dakle 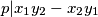 ,
, 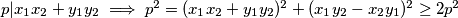
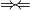
Napokon zakljucujemo da je nasa pocetna pretpostavka kriva i ne postoji takav  QED
QED
 Školjka
Školjka  prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina:
prirodan broj koji se može prikazivati kao suma kvadrata dvaju prirodnih brojeva na dva različita načina: