Točno
19. studenoga 2017. 13:13 (8 godine, 1 mjesec)
Let  be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 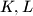 and
and  be the midpoints of the segments
be the midpoints of the segments 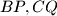 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 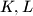 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 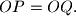
Proposed by Sergei Berlov, Russia
 be a triangle with circumcentre
be a triangle with circumcentre  . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 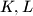 and
and  be the midpoints of the segments
be the midpoints of the segments 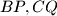 and
and  . respectively, and let
. respectively, and let  be the circle passing through
be the circle passing through 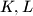 and
and  . Suppose that the line
. Suppose that the line  is tangent to the circle
is tangent to the circle  . Prove that
. Prove that 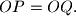
Proposed by Sergei Berlov, Russia
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Uočimo prvo da nam polovišta daju dosta informacija o konfiguraciji, imamo 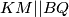 odnosno
odnosno 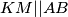 odakle slijedi
odakle slijedi 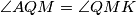 iz uvjeta tangentnosti
iz uvjeta tangentnosti 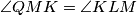 odnosno imamo slijedeće zaključke
odnosno imamo slijedeće zaključke 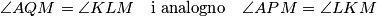
Što implicira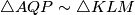
Pa povlačimo slijedeće odnose
Prvi odnos slijedi iz sličnosti danih trokuta, dok drugi slijedi iz prvobitnog zaključka o paralelnosti odnosno da je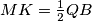 srednjica trokuta
srednjica trokuta 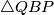 . Kombiniranjem dobivenog imamo
. Kombiniranjem dobivenog imamo 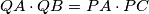 dakle
dakle  i
i  imaju jednaku potenciju na opisanu kružnicu
imaju jednaku potenciju na opisanu kružnicu  .
. 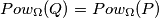
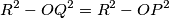
Odnosno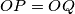
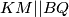 odnosno
odnosno 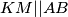 odakle slijedi
odakle slijedi 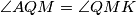 iz uvjeta tangentnosti
iz uvjeta tangentnosti 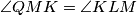 odnosno imamo slijedeće zaključke
odnosno imamo slijedeće zaključke 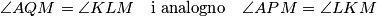
Što implicira
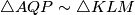
Pa povlačimo slijedeće odnose

Prvi odnos slijedi iz sličnosti danih trokuta, dok drugi slijedi iz prvobitnog zaključka o paralelnosti odnosno da je
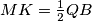 srednjica trokuta
srednjica trokuta 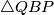 . Kombiniranjem dobivenog imamo
. Kombiniranjem dobivenog imamo 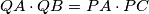 dakle
dakle  i
i  imaju jednaku potenciju na opisanu kružnicu
imaju jednaku potenciju na opisanu kružnicu  .
. 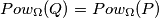
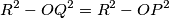
Odnosno
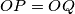
 Školjka
Školjka