IMO Shortlist 2009 problem G2
Kvaliteta:
Avg: 3,5Težina:
Avg: 6,0 Let  be a triangle with circumcentre
be a triangle with circumcentre 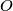 . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 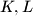 and
and  be the midpoints of the segments
be the midpoints of the segments 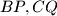 and
and 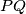 . respectively, and let
. respectively, and let 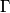 be the circle passing through
be the circle passing through 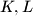 and
and  . Suppose that the line
. Suppose that the line 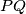 is tangent to the circle
is tangent to the circle 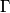 . Prove that
. Prove that 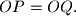
Proposed by Sergei Berlov, Russia
 be a triangle with circumcentre
be a triangle with circumcentre 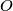 . The points
. The points  and
and  are interior points of the sides
are interior points of the sides  and
and  respectively. Let
respectively. Let 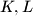 and
and  be the midpoints of the segments
be the midpoints of the segments 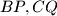 and
and 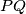 . respectively, and let
. respectively, and let 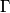 be the circle passing through
be the circle passing through 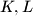 and
and  . Suppose that the line
. Suppose that the line 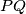 is tangent to the circle
is tangent to the circle 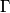 . Prove that
. Prove that 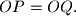
Proposed by Sergei Berlov, Russia
Izvor: Međunarodna matematička olimpijada, shortlist 2009
 Školjka
Školjka 
