Točno
13. ožujka 2018. 22:37 (7 godine, 11 mjeseci)
The numbers  ,
,  ,
,  ,
,  (
(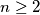 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 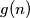 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 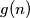 for every
for every  .
.
 ,
,  ,
,  ,
,  (
(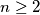 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 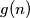 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 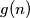 for every
for every  .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Tvrdimo da je 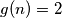 za sve potencije broja 2 a da je
za sve potencije broja 2 a da je 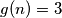 za sve ostale brojeve
za sve ostale brojeve
Jasno da je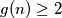 jer za
jer za  i
i  ne postoje brojevi koji čine tu artimetičku sredinu, pa je tako dovoljna konstrukcija za potencije broja 2 da bi na kraju
ne postoje brojevi koji čine tu artimetičku sredinu, pa je tako dovoljna konstrukcija za potencije broja 2 da bi na kraju 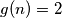
To činimo indukcijom po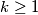 gdje je
gdje je 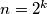
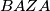
 je
je 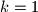 trivijalna
trivijalna
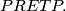
 da za neko
da za neko  vrijedi da
vrijedi da 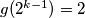
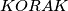
 od danih
od danih 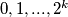 odaberemo interval
odaberemo interval 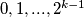 te pretpostavkom svedemo na brojeve
te pretpostavkom svedemo na brojeve 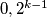 slično tako
slično tako 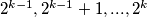 reduciramo u
reduciramo u 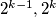 .
.
 Sada imamo
Sada imamo  broja
broja 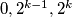 gdje je
gdje je 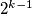 artimetička sredina
artimetička sredina  i
i  pa nam ga je dopušteno izbaciti. Tvrdnja je time dokazana.
pa nam ga je dopušteno izbaciti. Tvrdnja je time dokazana.
For the sake of contradiction, pretpostavimo da je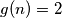 i za brojeve koje nisu potencije broja
i za brojeve koje nisu potencije broja  . U tom slučaju sa sigurnošću možemo tvrditi da su
. U tom slučaju sa sigurnošću možemo tvrditi da su 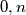 zadnji brojevi na ploči. Uzmimo neki prosti
zadnji brojevi na ploči. Uzmimo neki prosti 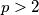 takav da
takav da  dijeli
dijeli  ( takav postoji jer smo pretpostavili da
( takav postoji jer smo pretpostavili da  nije potencija broja
nije potencija broja  ) uočimo da je artimetička sredina
) uočimo da je artimetička sredina  i
i  i dalje djeljiva sa
i dalje djeljiva sa  odnosno kako u artimetičkoj sredini samo dijelimo sa dvojkom zajednički djelitelj dva broja će ostati
odnosno kako u artimetičkoj sredini samo dijelimo sa dvojkom zajednički djelitelj dva broja će ostati  , tako bi backtrackingom dobili niz u kojem su svi članovi djeljivi sa
, tako bi backtrackingom dobili niz u kojem su svi članovi djeljivi sa  što dovodi do kontradikcije jer to ne zadovoljava početne uslove zadanog niza. Dakle
što dovodi do kontradikcije jer to ne zadovoljava početne uslove zadanog niza. Dakle 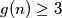 za ostale
za ostale  .
.
Kao konstrukciju posmatramo broj u obliku
u obliku 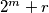 gdje je
gdje je 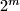 najveći pribrojnik koji je ujedno i potencija broja 2, uočimo da je
najveći pribrojnik koji je ujedno i potencija broja 2, uočimo da je 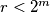 pa je u intervalu
pa je u intervalu 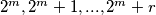 moguće obrisati članove tako da ostanu samo
moguće obrisati članove tako da ostanu samo 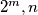 . Međutim znamo da
. Međutim znamo da 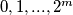 možemo reducirati u
možemo reducirati u 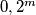 Tako zadani niz od
Tako zadani niz od  brojeva možemo reducirati u
brojeva možemo reducirati u  elementa
elementa 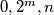 . Time je početna tvrdnja dokazana.
. Time je početna tvrdnja dokazana.
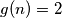 za sve potencije broja 2 a da je
za sve potencije broja 2 a da je 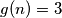 za sve ostale brojeve
za sve ostale brojeveJasno da je
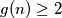 jer za
jer za  i
i  ne postoje brojevi koji čine tu artimetičku sredinu, pa je tako dovoljna konstrukcija za potencije broja 2 da bi na kraju
ne postoje brojevi koji čine tu artimetičku sredinu, pa je tako dovoljna konstrukcija za potencije broja 2 da bi na kraju 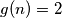
To činimo indukcijom po
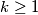 gdje je
gdje je 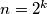
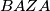
 je
je 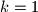 trivijalna
trivijalna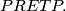
 da za neko
da za neko  vrijedi da
vrijedi da 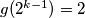
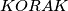
 od danih
od danih 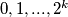 odaberemo interval
odaberemo interval 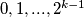 te pretpostavkom svedemo na brojeve
te pretpostavkom svedemo na brojeve 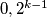 slično tako
slično tako 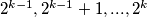 reduciramo u
reduciramo u 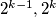 .
. Sada imamo
Sada imamo  broja
broja 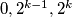 gdje je
gdje je 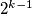 artimetička sredina
artimetička sredina  i
i  pa nam ga je dopušteno izbaciti. Tvrdnja je time dokazana.
pa nam ga je dopušteno izbaciti. Tvrdnja je time dokazana.For the sake of contradiction, pretpostavimo da je
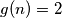 i za brojeve koje nisu potencije broja
i za brojeve koje nisu potencije broja  . U tom slučaju sa sigurnošću možemo tvrditi da su
. U tom slučaju sa sigurnošću možemo tvrditi da su 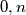 zadnji brojevi na ploči. Uzmimo neki prosti
zadnji brojevi na ploči. Uzmimo neki prosti 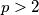 takav da
takav da  dijeli
dijeli  ( takav postoji jer smo pretpostavili da
( takav postoji jer smo pretpostavili da  nije potencija broja
nije potencija broja  ) uočimo da je artimetička sredina
) uočimo da je artimetička sredina  i
i  i dalje djeljiva sa
i dalje djeljiva sa  odnosno kako u artimetičkoj sredini samo dijelimo sa dvojkom zajednički djelitelj dva broja će ostati
odnosno kako u artimetičkoj sredini samo dijelimo sa dvojkom zajednički djelitelj dva broja će ostati  , tako bi backtrackingom dobili niz u kojem su svi članovi djeljivi sa
, tako bi backtrackingom dobili niz u kojem su svi članovi djeljivi sa  što dovodi do kontradikcije jer to ne zadovoljava početne uslove zadanog niza. Dakle
što dovodi do kontradikcije jer to ne zadovoljava početne uslove zadanog niza. Dakle 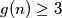 za ostale
za ostale  .
.Kao konstrukciju posmatramo broj
 u obliku
u obliku 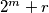 gdje je
gdje je 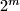 najveći pribrojnik koji je ujedno i potencija broja 2, uočimo da je
najveći pribrojnik koji je ujedno i potencija broja 2, uočimo da je 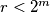 pa je u intervalu
pa je u intervalu 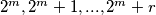 moguće obrisati članove tako da ostanu samo
moguće obrisati članove tako da ostanu samo 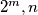 . Međutim znamo da
. Međutim znamo da 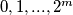 možemo reducirati u
možemo reducirati u 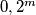 Tako zadani niz od
Tako zadani niz od  brojeva možemo reducirati u
brojeva možemo reducirati u  elementa
elementa 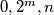 . Time je početna tvrdnja dokazana.
. Time je početna tvrdnja dokazana.  Školjka
Školjka