MEMO 2009 ekipno problem 3
Kvaliteta:
Avg: 3,0Težina:
Avg: 5,0 The numbers  ,
,  ,
,  ,
,  (
(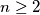 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 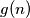 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 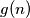 for every
for every  .
.
 ,
,  ,
,  ,
,  (
(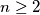 ) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let
) are written on a blackboard. In each step we erase an integer which is the arithmetic mean of two different numbers which are still left on the blackboard. We make such steps until no further integer can be erased. Let 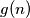 be the smallest possible number of integers left on the blackboard at the end. Find
be the smallest possible number of integers left on the blackboard at the end. Find 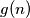 for every
for every  .
. Izvor: Srednjoeuropska matematička olimpijada 2009, ekipno natjecanje, problem 3
 Školjka
Školjka 
