Točno
17. ožujka 2018. 14:46 (7 godine, 12 mjeseci)
Dan je šiljastokutni trokut  u kojem vrijedi
u kojem vrijedi 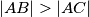 . Neka je
. Neka je  središte kružnice opisane tom trokutu, a
središte kružnice opisane tom trokutu, a 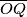 promjer kružnice opisane trokutu
promjer kružnice opisane trokutu 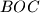 . Pravac paralelan s pravcem
. Pravac paralelan s pravcem  kroz
kroz  siječe pravac
siječe pravac 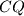 u točki
u točki  , a pravac paralelan s pravcem
, a pravac paralelan s pravcem 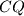 kroz
kroz  siječe pravac
siječe pravac  u točki
u točki  . Neka je
. Neka je  presjek pravaca
presjek pravaca 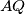 i
i  . Dokaži da točka
. Dokaži da točka  leži na kružnici opisanoj trokutu
leži na kružnici opisanoj trokutu 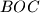 .
.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je  presjek
presjek 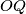 i
i  . Kako su
. Kako su 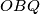 i
i 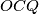 trivijalno sukladni slijedi da je
trivijalno sukladni slijedi da je  polovište
polovište  . Neka je
. Neka je  presjek
presjek  i
i  . Kako je
. Kako je 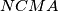 paralelogram je
paralelogram je  polovište
polovište  .
.
Lako se dobije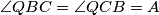 pa su
pa su 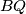 i
i 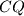 tangente na
tangente na 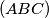 . Tada je
. Tada je 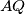 simedijana
simedijana  te po njenoj definiciji
te po njenoj definiciji 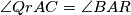 .
.
Dobije se i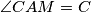 i
i 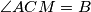 iz čega slijedi da su
iz čega slijedi da su  i
i 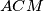 slični. Kako je
slični. Kako je 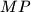 težišnica
težišnica 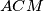 slijedi
slijedi 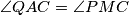 .
.
Zaključujemo da je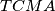 tetivan pa je
tetivan pa je 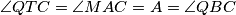 te su zatim
te su zatim 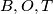 i
i  konciklične.
konciklične. 
 presjek
presjek 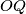 i
i  . Kako su
. Kako su 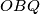 i
i 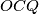 trivijalno sukladni slijedi da je
trivijalno sukladni slijedi da je  polovište
polovište  . Neka je
. Neka je  presjek
presjek  i
i  . Kako je
. Kako je 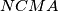 paralelogram je
paralelogram je  polovište
polovište  .
.Lako se dobije
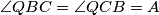 pa su
pa su 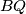 i
i 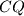 tangente na
tangente na 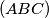 . Tada je
. Tada je 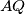 simedijana
simedijana  te po njenoj definiciji
te po njenoj definiciji 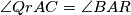 .
.Dobije se i
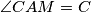 i
i 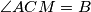 iz čega slijedi da su
iz čega slijedi da su  i
i 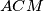 slični. Kako je
slični. Kako je 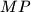 težišnica
težišnica 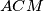 slijedi
slijedi 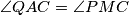 .
.Zaključujemo da je
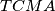 tetivan pa je
tetivan pa je 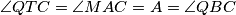 te su zatim
te su zatim 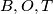 i
i  konciklične.
konciklične. 
 Školjka
Školjka