Sakrij rješenje
Dokaži da je broj jedinica u svim neuređenim particijama nekog prirodnog broja jednak:
a) sumi brojeva različitih elemenata po svim particijama
b) sumi razlika, po svim particijama, najvećeg i drugog po veličini elementa
Neuređena particija prirodnog broja  je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata
je multiskup prirodnih brojeva takav da je zbroj njegovih elemenata  .
.
(Ivan Novak, Borna Šimić)
Kliknite ovdje kako biste prikazali rješenje.
a)
Za prirodan broj  , označimo s
, označimo s 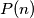 broj neuređenih particija broja
broj neuređenih particija broja  , te označimo s
, te označimo s 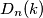 broj particija broja
broj particija broja  koje sadrže barem
koje sadrže barem  jedinica. Uočimo da je broj particija koje sadrže točno
jedinica. Uočimo da je broj particija koje sadrže točno  jedinica tada jednak
jedinica tada jednak 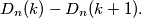
Promotrimo neku particiju broja  koja sadrži barem
koja sadrži barem  jedinica. Uklanjanjem tih
jedinica. Uklanjanjem tih  jedinica iz particije, generiramo particiju broja
jedinica iz particije, generiramo particiju broja 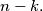 Analogno, svakoj particiji broja
Analogno, svakoj particiji broja 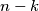 možemo dodati
možemo dodati  jedinica i generirati particiju broja
jedinica i generirati particiju broja  koja sadrži barem
koja sadrži barem  jedinica. Prema tome, između skupa particija broja
jedinica. Prema tome, između skupa particija broja  s barem
s barem  jedinica i skupa particija broja
jedinica i skupa particija broja 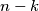 postoji bijekcija. Iz toga slijedi
postoji bijekcija. Iz toga slijedi 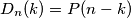
Prema tome, broj jedinica u svim particijama iznosi 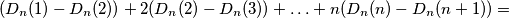
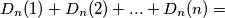
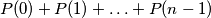
Označimo s 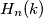 broj particija broja
broj particija broja  u kojima se pojavljuje broj
u kojima se pojavljuje broj  . Uočimo da je suma brojeva različitih elemenata po svim particijama jednaka
. Uočimo da je suma brojeva različitih elemenata po svim particijama jednaka 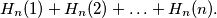
Promotrimo particiju broja  u kojoj se pojavljuje broj
u kojoj se pojavljuje broj  . Uklanjanjem broja
. Uklanjanjem broja  generiramo particiju broja
generiramo particiju broja 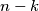 . Obratno, dodavanjem
. Obratno, dodavanjem  particiji broja
particiji broja 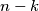 generiramo particiju broja
generiramo particiju broja  koja sadrži
koja sadrži  . Iz ovog zaključujemo da postoji bijekcija između skupa particija broja
. Iz ovog zaključujemo da postoji bijekcija između skupa particija broja 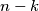 i skupa particija broja
i skupa particija broja  koje sadrže
koje sadrže  . Prema tome, imamo
. Prema tome, imamo 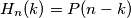 , iz čega slijedi
, iz čega slijedi 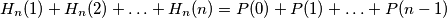 što je i trebalo dokazati.
što je i trebalo dokazati.
b)
Prikažimo neuređene particije prirodnih brojeva dijagramom na sljedeći način: poredajmo brojeve unutar particije od najvećeg prema najmanjem i za svakog člana particije u vlastiti redak postavimo onoliko kvadratića koliko je on velik. Primijetimo sljedeću bijekciju na skupu particija: preslikamo cijeli dijagram preko pravca na kojem leži glavna dijagonala prvog kvadratića.
Ova bijekcija slika razliku najvećeg i drugog po veličini člana jedne particije u sve jedinice njoj pridružene particije, pa je time i suma svih razlika jednaka sumi broja jedinica po svim particijama, što je i trebalo pokazati.
 Školjka
Školjka