Točno
18. travnja 2012. 21:52 (13 godine, 10 mjeseci)
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
Neka je <ABC=<ACB=y i neka je <ABP=<BCP=x.
Lako se naganjenjem kuteva dobije <DPC=y, <ACP=y-x, <ADP=2y-x, <APD=90-y, <PAC=90-(y-x), itd.
Primjenom sinusovog poučka na stranice |AD| i |PD| trokuta APD te sinusovog poučka na stranice |CD| i |PD| trokuta CPD;
a zatim dijeljem tih jednadžbi (da se poništi |PD|) dobije se:
|AD| : |CD|=(sin(90-y)*sin(y-x)) : (sin(90-(y-x))*sin(y)) = (cos(y)*sin(y-x)) : (cos(y-x)*sin(y)).
Zbog formule za pretvorbu umnoška u zbroj ( ... sin(a)cos(b) = 1/2( sin(a+b)+sin(a-b) ) ... ) možemo pisati:
|AD| : |CD|=(sin(2y-x)-sinx) : (sin(2y-x)+sinx)). ( ... gdje smo koristili sin(-x) = -sin(x) ...)
Ako brojnik i nazivnik podijelimo sa sinx dobijemo:
(1) |AD| : |CD|=(sin(2y-x)/sinx - 1) : (sin(2y-x)/sinx + 1))
Stavimo |AD| : |CD|=t. Zbog sinusovog poučka na trokut ABD vidimo da je
sin(2y-x):sinx=|AB|:|AD|=(|AD|+|CD|):|AD|=(1+1/t).
Sada (1) možemo zapisati kao t = (1/t) : (2+1/t).
Dobijemo kvadratnu jednadžbu 2*t^2 + t - 1=0 čije je poz. rješenje t=1/2 (negativno je očito t=-1).
|AD| : |CD|=t=1/2.
(žao mi je što ne znam latex niti imam vremena ga naučiti)
Lako se naganjenjem kuteva dobije <DPC=y, <ACP=y-x, <ADP=2y-x, <APD=90-y, <PAC=90-(y-x), itd.
Primjenom sinusovog poučka na stranice |AD| i |PD| trokuta APD te sinusovog poučka na stranice |CD| i |PD| trokuta CPD;
a zatim dijeljem tih jednadžbi (da se poništi |PD|) dobije se:
|AD| : |CD|=(sin(90-y)*sin(y-x)) : (sin(90-(y-x))*sin(y)) = (cos(y)*sin(y-x)) : (cos(y-x)*sin(y)).
Zbog formule za pretvorbu umnoška u zbroj ( ... sin(a)cos(b) = 1/2( sin(a+b)+sin(a-b) ) ... ) možemo pisati:
|AD| : |CD|=(sin(2y-x)-sinx) : (sin(2y-x)+sinx)). ( ... gdje smo koristili sin(-x) = -sin(x) ...)
Ako brojnik i nazivnik podijelimo sa sinx dobijemo:
(1) |AD| : |CD|=(sin(2y-x)/sinx - 1) : (sin(2y-x)/sinx + 1))
Stavimo |AD| : |CD|=t. Zbog sinusovog poučka na trokut ABD vidimo da je
sin(2y-x):sinx=|AB|:|AD|=(|AD|+|CD|):|AD|=(1+1/t).
Sada (1) možemo zapisati kao t = (1/t) : (2+1/t).
Dobijemo kvadratnu jednadžbu 2*t^2 + t - 1=0 čije je poz. rješenje t=1/2 (negativno je očito t=-1).
|AD| : |CD|=t=1/2.
(žao mi je što ne znam latex niti imam vremena ga naučiti)
 Školjka
Školjka  vrijedi
vrijedi 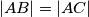 . Na stranici
. Na stranici  nalazi se točka
nalazi se točka  takva da je
takva da je 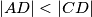 , a na dužini
, a na dužini  točka
točka  takva da je
takva da je 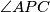 pravi kut. Ako je
pravi kut. Ako je 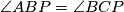 , odredi
, odredi 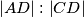 .
.