Skica: https://i.imgur.com/p5mBDRC.png
Neka je točka  definirana kao u zadatku. Neka kružnica
definirana kao u zadatku. Neka kružnica 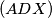 siječe stranicu
siječe stranicu  u
u  i neka kružnica
i neka kružnica 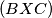 siječe stranicu
siječe stranicu  u
u  . Neka je drugi presjek kružnica
. Neka je drugi presjek kružnica 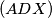 i
i 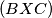 točka Y. Dokaz ćemo podijeliti u tri dijela:
točka Y. Dokaz ćemo podijeliti u tri dijela: 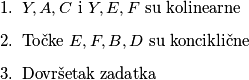
1. Uočimo da se zbog tetivnosti i danih relacija o kutevima trivijalno može dobiti 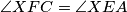 i
i 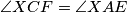 . Iz toga slijedi
. Iz toga slijedi 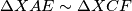 pa su oni i spiralno slični. Iz svojstava spiralne sličnosti sada znamo da je točka
pa su oni i spiralno slični. Iz svojstava spiralne sličnosti sada znamo da je točka  na pravcima
na pravcima  i
i  .
.
2. Uočimo da još uvijek nismo iskoristili uvjet za četverokut  . Poznato je da je dani uvjet ekvivalentan s time da se simetrale kutova
. Poznato je da je dani uvjet ekvivalentan s time da se simetrale kutova 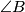 i
i 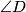 sijeku na
sijeku na  . Neka su ti presjeci
. Neka su ti presjeci  i
i  . Napravimo kružnicu
. Napravimo kružnicu  kroz točke
kroz točke 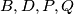 (te 4 točke su konciklične jer simetrale unutarnjeg i vanjskog kuta iz vrha trokuta zatvaraju kut od
(te 4 točke su konciklične jer simetrale unutarnjeg i vanjskog kuta iz vrha trokuta zatvaraju kut od 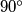 ). Sada je jasno da je
). Sada je jasno da je  zapravo
zapravo  , odnosno
, odnosno  Apolonijeva kružnica trokuta
Apolonijeva kružnica trokuta  odnosno
odnosno  . Neka je
. Neka je  središte kružnice
središte kružnice  . Poznata lema kaže da
. Poznata lema kaže da 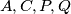 harmonik, a druga poznata lema kaže da iz toga slijedi
harmonik, a druga poznata lema kaže da iz toga slijedi 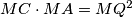 . Sljedeća stvar koju želimo pokazati jest da su
. Sljedeća stvar koju želimo pokazati jest da su 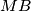 i
i 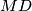 tangente na kružnice
tangente na kružnice 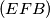 i
i 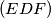 što bi nam dalo da su točke
što bi nam dalo da su točke 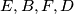 konciklične.
konciklične. 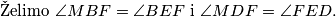 Sada ćemo nizom jednakosti između kutova pokazati željene tvrdnje.
Sada ćemo nizom jednakosti između kutova pokazati željene tvrdnje. 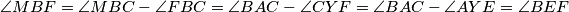 gdje je
gdje je 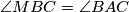 zbog činjenice da je
zbog činjenice da je 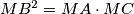 i
i 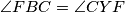 zbog tetivnosti. Nadalje
zbog tetivnosti. Nadalje 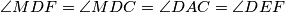 gdje je
gdje je 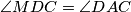 zbog
zbog 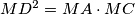 i
i 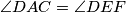 zbog tetivnosti. Sada imamo da su kružnice
zbog tetivnosti. Sada imamo da su kružnice 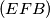 i
i 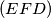 ortogonalne s kružnicom
ortogonalne s kružnicom  , no kako je kružnica kroz dvije točke ortogonalna na neku drugu jedinstvena, dobivamo da je
, no kako je kružnica kroz dvije točke ortogonalna na neku drugu jedinstvena, dobivamo da je 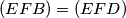 odnosno da su točke
odnosno da su točke 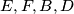 konciklične.
konciklične.
3. Sada još preostaje pokazati da je 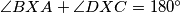 . Uočimo da je to ekvivalentno da pokažemo da je
. Uočimo da je to ekvivalentno da pokažemo da je 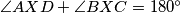 odnosno, da je
odnosno, da je 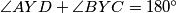 , a to je naposljetku ekvivalnento s time da je
, a to je naposljetku ekvivalnento s time da je 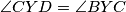 odnosno da je
odnosno da je 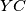 simetrala kuta
simetrala kuta 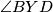 . Prenošenjem obodnih kuteva po kružnici dobivamo da je
. Prenošenjem obodnih kuteva po kružnici dobivamo da je 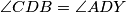 pa su
pa su  i
i 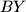 izogonalne u kutu
izogonalne u kutu 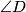 , odnosno,
, odnosno, 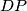 je simetrala kuta
je simetrala kuta 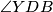 . Analogno se dobije da je
. Analogno se dobije da je 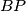 simetrala kuta
simetrala kuta 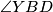 pa je
pa je  centar upisane kružnice trokuta
centar upisane kružnice trokuta 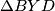 pa je
pa je 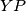 simetrala kuta, odnosno,
simetrala kuta, odnosno, 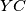 je simetrala kuta
je simetrala kuta 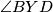 što je trebalo i dokazati.
što je trebalo i dokazati.
Skica: \url{https://i.imgur.com/p5mBDRC.png}
\\
\\
\\
Neka je točka $X$ definirana kao u zadatku. Neka kružnica $(ADX)$ siječe stranicu $AB$ u $E$ i neka kružnica $(BXC)$ siječe stranicu $CD$ u $F$. Neka je drugi presjek kružnica $(ADX)$ i $(BXC)$ točka Y. Dokaz ćemo podijeliti u tri dijela: \begin{enumerate} \item $Y,A,C$ i $Y,E,F$ su kolinearne \item Točke $E,F,B,D$ su konciklične \item Dovršetak zadatka \end{enumerate}
1. Uočimo da se zbog tetivnosti i danih relacija o kutevima trivijalno može dobiti $\angle{XFC} = \angle{XEA}$ i $\angle{XCF} = \angle{XAE}$. Iz toga slijedi $\Delta XAE \sim \Delta XCF$ pa su oni i spiralno slični. Iz svojstava spiralne sličnosti sada znamo da je točka $Y$ na pravcima $AC$ i $EF$.\\ \\
2. Uočimo da još uvijek nismo iskoristili uvjet za četverokut $ABCD$. Poznato je da je dani uvjet ekvivalentan s time da se simetrale kutova $\angle{B}$ i $\angle{D}$ sijeku na $AC$. Neka su ti presjeci $P$ i $Q$. Napravimo kružnicu $\omega$ kroz točke $B,D,P,Q$ (te 4 točke su konciklične jer simetrale unutarnjeg i vanjskog kuta iz vrha trokuta zatvaraju kut od $90^\circ$). Sada je jasno da je $\omega$ zapravo $B$, odnosno $D$
Apolonijeva kružnica trokuta $ABC$ odnosno $ACD$. Neka je $M$ središte kružnice $\omega$. Poznata lema kaže da $A,C,P,Q$ harmonik, a druga poznata lema kaže da iz toga slijedi $MC \cdot MA = MQ^2$. Sljedeća stvar koju želimo pokazati jest da su $MB$ i $MD$ tangente na kružnice $(EFB)$ i $(EDF)$ što bi nam dalo da su točke $E,B,F,D$ konciklične. \[\text{Želimo } \angle{MBF} = \angle{BEF} \text{ i } \angle{MDF} = \angle{FED}.\] Sada ćemo nizom jednakosti između kutova pokazati željene tvrdnje.
\[\angle{MBF} = \angle{MBC} - \angle{FBC} = \angle{BAC} - \angle{CYF} = \angle{BAC} - \angle{AYE} = \angle{BEF}\] gdje je $\angle{MBC} = \angle{BAC}$ zbog činjenice da je $MB^2 = MA \cdot MC$ i $\angle{FBC} = \angle{CYF}$ zbog tetivnosti. Nadalje
\[\angle{MDF} = \angle{MDC} = \angle{DAC} = \angle{DEF}\] gdje je $\angle{MDC} = \angle{DAC}$ zbog $MD^2 = MA \cdot MC$ i $\angle{DAC} = \angle{DEF}$ zbog tetivnosti. Sada imamo da su kružnice $(EFB)$ i $(EFD)$ ortogonalne s kružnicom $\omega$, no kako je kružnica kroz dvije točke ortogonalna na neku drugu jedinstvena, dobivamo da je $(EFB) = (EFD)$ odnosno da su točke $E,F,B,D$ konciklične.\\ \\
3. Sada još preostaje pokazati da je $\angle{BXA} + \angle{DXC} = 180^\circ$. Uočimo da je to ekvivalentno da pokažemo da je $\angle{AXD} + \angle{BXC} = 180^\circ$ odnosno, da je $\angle{AYD} + \angle{BYC} = 180^\circ$, a to je naposljetku ekvivalnento s time da je $\angle{CYD} = \angle{BYC}$ odnosno da je $YC$ simetrala kuta $\angle{BYD}$. Prenošenjem obodnih kuteva po kružnici dobivamo da je $\angle{CDB} = \angle{ADY}$ pa su $BD$ i $BY$ izogonalne u kutu $\angle{D}$, odnosno, $DP$ je simetrala kuta $\angle{YDB}$. Analogno se dobije da je $BP$ simetrala kuta $\angle{YBD}$ pa je $P$ centar upisane kružnice trokuta $\Delta BYD$ pa je $YP$ simetrala kuta, odnosno, $YC$ je simetrala kuta $\angle{BYD}$ što je trebalo i dokazati.
 definirana kao u zadatku. Neka kružnica
definirana kao u zadatku. Neka kružnica 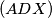 siječe stranicu
siječe stranicu  u
u  i neka kružnica
i neka kružnica 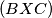 siječe stranicu
siječe stranicu  u
u  . Neka je drugi presjek kružnica
. Neka je drugi presjek kružnica 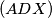 i
i 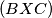 točka Y. Dokaz ćemo podijeliti u tri dijela:
točka Y. Dokaz ćemo podijeliti u tri dijela: 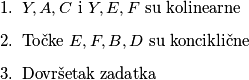
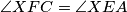 i
i 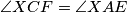 . Iz toga slijedi
. Iz toga slijedi 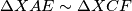 pa su oni i spiralno slični. Iz svojstava spiralne sličnosti sada znamo da je točka
pa su oni i spiralno slični. Iz svojstava spiralne sličnosti sada znamo da je točka  na pravcima
na pravcima  i
i  .
. . Poznato je da je dani uvjet ekvivalentan s time da se simetrale kutova
. Poznato je da je dani uvjet ekvivalentan s time da se simetrale kutova 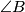 i
i 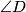 sijeku na
sijeku na  . Neka su ti presjeci
. Neka su ti presjeci  i
i  . Napravimo kružnicu
. Napravimo kružnicu  kroz točke
kroz točke 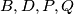 (te 4 točke su konciklične jer simetrale unutarnjeg i vanjskog kuta iz vrha trokuta zatvaraju kut od
(te 4 točke su konciklične jer simetrale unutarnjeg i vanjskog kuta iz vrha trokuta zatvaraju kut od 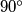 ). Sada je jasno da je
). Sada je jasno da je  zapravo
zapravo  , odnosno
, odnosno  Apolonijeva kružnica trokuta
Apolonijeva kružnica trokuta  odnosno
odnosno  . Neka je
. Neka je  središte kružnice
središte kružnice  . Poznata lema kaže da
. Poznata lema kaže da 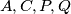 harmonik, a druga poznata lema kaže da iz toga slijedi
harmonik, a druga poznata lema kaže da iz toga slijedi 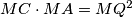 . Sljedeća stvar koju želimo pokazati jest da su
. Sljedeća stvar koju želimo pokazati jest da su 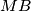 i
i 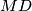 tangente na kružnice
tangente na kružnice 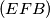 i
i 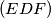 što bi nam dalo da su točke
što bi nam dalo da su točke 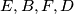 konciklične.
konciklične. 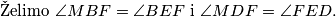 Sada ćemo nizom jednakosti između kutova pokazati željene tvrdnje.
Sada ćemo nizom jednakosti između kutova pokazati željene tvrdnje. 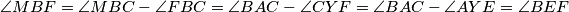 gdje je
gdje je 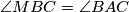 zbog činjenice da je
zbog činjenice da je 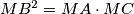 i
i 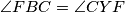 zbog tetivnosti. Nadalje
zbog tetivnosti. Nadalje 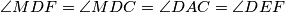 gdje je
gdje je 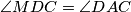 zbog
zbog 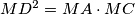 i
i 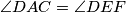 zbog tetivnosti. Sada imamo da su kružnice
zbog tetivnosti. Sada imamo da su kružnice 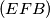 i
i 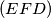 ortogonalne s kružnicom
ortogonalne s kružnicom  , no kako je kružnica kroz dvije točke ortogonalna na neku drugu jedinstvena, dobivamo da je
, no kako je kružnica kroz dvije točke ortogonalna na neku drugu jedinstvena, dobivamo da je 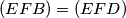 odnosno da su točke
odnosno da su točke 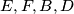 konciklične.
konciklične.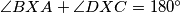 . Uočimo da je to ekvivalentno da pokažemo da je
. Uočimo da je to ekvivalentno da pokažemo da je 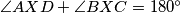 odnosno, da je
odnosno, da je 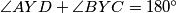 , a to je naposljetku ekvivalnento s time da je
, a to je naposljetku ekvivalnento s time da je 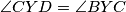 odnosno da je
odnosno da je 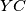 simetrala kuta
simetrala kuta 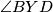 . Prenošenjem obodnih kuteva po kružnici dobivamo da je
. Prenošenjem obodnih kuteva po kružnici dobivamo da je 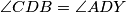 pa su
pa su  i
i 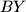 izogonalne u kutu
izogonalne u kutu 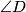 , odnosno,
, odnosno, 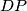 je simetrala kuta
je simetrala kuta 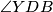 . Analogno se dobije da je
. Analogno se dobije da je 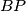 simetrala kuta
simetrala kuta 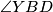 pa je
pa je  centar upisane kružnice trokuta
centar upisane kružnice trokuta 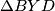 pa je
pa je 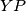 simetrala kuta, odnosno,
simetrala kuta, odnosno, 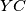 je simetrala kuta
je simetrala kuta 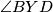 što je trebalo i dokazati.
što je trebalo i dokazati.  Školjka
Školjka 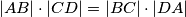 . Točka
. Točka 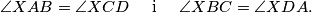 Dokaži da je
Dokaži da je