Neocijenjeno
14. svibnja 2019. 21:32 (6 godine, 10 mjeseci)
Two circles
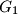
and
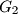
intersect at two points

and

. Let

be the line tangent to these circles at

and

, respectively, so that

lies closer to

than

. Let

be the line parallel to

and passing through the point

, with

on
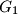
and

on
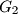
. Lines

and

meet at

; lines
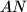
and

meet at

; lines
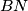
and

meet at

. Show that
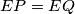
.
%V0
Two circles $G_1$ and $G_2$ intersect at two points $M$ and $N$. Let $AB$ be the line tangent to these circles at $A$ and $B$, respectively, so that $M$ lies closer to $AB$ than $N$. Let $CD$ be the line parallel to $AB$ and passing through the point $M$, with $C$ on $G_1$ and $D$ on $G_2$. Lines $AC$ and $BD$ meet at $E$; lines $AN$ and $CD$ meet at $P$; lines $BN$ and $CD$ meet at $Q$. Show that $EP = EQ$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka je K presjek prave AB sa NM.Primjetimo da je KA^2=KM*KN=KB^2.To jeste KA = KB,a to znači da je K središte AB,Zbog AB || CD važi da je i M središte PQ.
Ugao BAM je jednak uglu ACM ,a zbog paralelnosti on je jednak uglu EAB.Slično ugao ABM je jednak uglu BDM, a zbog paralelnosti on je jednak uglu EBA. Sada znamo da su E i M simetrične u odnosu na pravu AB.
EM je okomito na AB,a iz uslova zadatka znamo da je AB paralelno sa PQ,to znači da su trouglovi EMP I EMQ podudarni,a to znači da je EP=EQ.
Q.E.D
Neka je K presjek prave AB sa NM.Primjetimo da je KA^2=KM*KN=KB^2.To jeste KA = KB,a to znači da je K središte AB,Zbog AB || CD važi da je i M središte PQ.
Ugao BAM je jednak uglu ACM ,a zbog paralelnosti on je jednak uglu EAB.Slično ugao ABM je jednak uglu BDM, a zbog paralelnosti on je jednak uglu EBA.
Sada znamo da su E i M simetrične u odnosu na pravu AB.
EM je okomito na AB,a iz uslova zadatka znamo da je AB paralelno sa PQ,to znači da su trouglovi EMP I EMQ podudarni,a to znači da je EP=EQ.
Q.E.D
 Školjka
Školjka 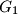 and
and 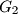 intersect at two points
intersect at two points  and
and  . Let
. Let  be the line tangent to these circles at
be the line tangent to these circles at  and
and  , respectively, so that
, respectively, so that  be the line parallel to
be the line parallel to  on
on  on
on  and
and  meet at
meet at  ; lines
; lines 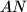 and
and  ; lines
; lines 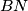 and
and  . Show that
. Show that 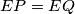 .
.