IMO Shortlist 2000 problem G2
Dodao/la:
arhiva2. travnja 2012. Two circles
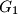
and
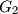
intersect at two points

and

. Let

be the line tangent to these circles at

and

, respectively, so that

lies closer to

than

. Let

be the line parallel to

and passing through the point

, with

on
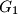
and

on
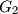
. Lines

and

meet at

; lines
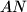
and

meet at

; lines
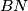
and

meet at

. Show that
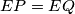
.
%V0
Two circles $G_1$ and $G_2$ intersect at two points $M$ and $N$. Let $AB$ be the line tangent to these circles at $A$ and $B$, respectively, so that $M$ lies closer to $AB$ than $N$. Let $CD$ be the line parallel to $AB$ and passing through the point $M$, with $C$ on $G_1$ and $D$ on $G_2$. Lines $AC$ and $BD$ meet at $E$; lines $AN$ and $CD$ meet at $P$; lines $BN$ and $CD$ meet at $Q$. Show that $EP = EQ$.
Izvor: Međunarodna matematička olimpijada, shortlist 2000