Neocijenjeno
25. rujna 2019. 23:34 (6 godine, 3 mjeseci)
Neka je $M$ polovište stranice $AC$ u šiljastokutnom trokutu $ABC$ u kojem vrijedi $AB>BC$. Neka je $\Omega $ opisana kružnica trokuta $ ABC$. Tangenta na $ \Omega $ u točkama $A$ i $C$ se sijeku u $P$, a $BP$ i $AC$ se sijeku u $S$. Neka je $AD$ visina u trokutu $ABP$, a $\omega$ opisana kružnica trokuta $CSD$. Pretpostavite da se $ \omega$ i $ \Omega $ sijeku u $K\not= C$. Dokažite: $ \angle CKM=90^\circ $.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Since 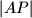 =
=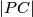 , we have
, we have 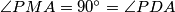 , so
, so 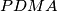 is cyclic, and let it be
is cyclic, and let it be  . Let
. Let  be the intersection of
be the intersection of 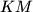 with
with  . That means, that it is enough to prove that
. That means, that it is enough to prove that 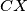 is the diameter of
is the diameter of  . Since
. Since 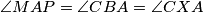 , and we want
, and we want 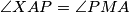 , we want triangles
, we want triangles 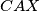 and
and 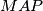 to be similar, so we want
to be similar, so we want 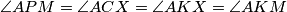 , but that is equivalent of proving that
, but that is equivalent of proving that 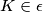 . Let
. Let  be the intersection of
be the intersection of 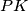 and
and  . By the symmedian theorem we know that
. By the symmedian theorem we know that 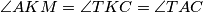 , so
, so 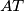 is tangent to
is tangent to  . But as
. But as 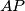 is the diameter of
is the diameter of  , that means
, that means 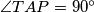 . So
. So 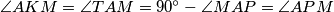 , so
, so 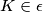 .
.
Since $|AP|$=$|PC|$, we have $\angle PMA=90^{\circ}=\angle PDA$, so $PDMA$ is cyclic, and let it be $\epsilon$. Let $X$ be the intersection of $KM$ with $\omega$. That means, that it is enough to prove that $CX$ is the diameter of $\omega$. Since $\angle MAP=\angle CBA=\angle CXA$, and we want $\angle XAP=\angle PMA$, we want triangles $CAX$ and $MAP$ to be similar, so we want $\angle APM=\angle ACX=\angle AKX=\angle AKM$, but that is equivalent of proving that $K \in \epsilon$. Let $T$ be the intersection of $PK$ and $\omega$. By the symmedian theorem we know that $\angle AKM=\angle TKC=\angle TAC$, so $AT$ is tangent to $\epsilon$. But as $AP$ is the diameter of $\epsilon$, that means $\angle TAP=90^{\circ}$. So $\angle AKM=\angle TAM= 90^{\circ}- \angle MAP=\angle APM$, so $K \in \epsilon$.
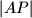 =
=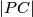 , we have
, we have 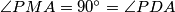 , so
, so 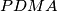 is cyclic, and let it be
is cyclic, and let it be  . Let
. Let  be the intersection of
be the intersection of 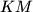 with
with  . That means, that it is enough to prove that
. That means, that it is enough to prove that 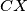 is the diameter of
is the diameter of  . Since
. Since 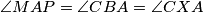 , and we want
, and we want 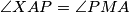 , we want triangles
, we want triangles 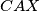 and
and 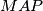 to be similar, so we want
to be similar, so we want 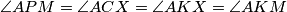 , but that is equivalent of proving that
, but that is equivalent of proving that 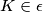 . Let
. Let  be the intersection of
be the intersection of 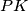 and
and  . By the symmedian theorem we know that
. By the symmedian theorem we know that 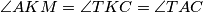 , so
, so 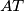 is tangent to
is tangent to  . But as
. But as 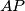 is the diameter of
is the diameter of  , that means
, that means 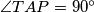 . So
. So 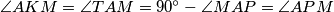 , so
, so 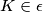 .
.  Školjka
Školjka  polovište stranice
polovište stranice  u šiljastokutnom trokutu
u šiljastokutnom trokutu  u kojem vrijedi
u kojem vrijedi 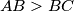 . Neka je
. Neka je  opisana kružnica trokuta
opisana kružnica trokuta  i
i  se sijeku u
se sijeku u  , a
, a 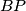 i
i  . Neka je
. Neka je  visina u trokutu
visina u trokutu 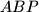 , a
, a 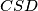 . Pretpostavite da se
. Pretpostavite da se 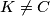 . Dokažite:
. Dokažite: 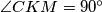 .
.