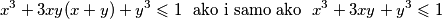Prvo rješenje. (Borna Šimić)
Prva nejednakost je 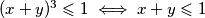 . Međutim, imamo
. Međutim, imamo 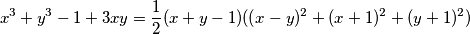 pa su nejednakosti očito ekvivalentne.
pa su nejednakosti očito ekvivalentne.
Drugo rješenje. (Ivan Novak)
Razlikujemo  slučaja:
slučaja: 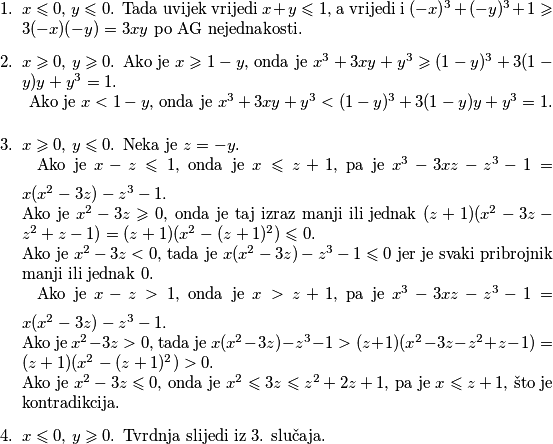
Treće rješenje. (Ivan Novak)
Prva nejednakost je ekvivalentna s 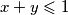 . Dovoljno je dokazati
. Dovoljno je dokazati 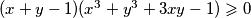 . Sada vrijedi niz ekvivalencija:
. Sada vrijedi niz ekvivalencija: 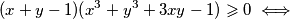
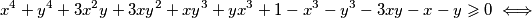
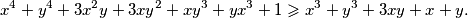 Uvedimo supstituciju
Uvedimo supstituciju 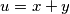 ,
, 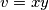 . Tada zadnju nejednakost možemo zapisati kao
. Tada zadnju nejednakost možemo zapisati kao 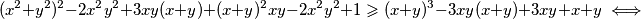
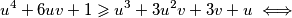
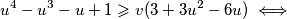
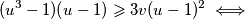
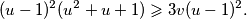 Ako je
Ako je 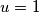 , nejednakost je očita. Ako nije, tada je dovoljno pokazati
, nejednakost je očita. Ako nije, tada je dovoljno pokazati 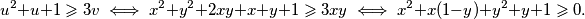 Ako izraz gledamo kao kvadratnu funkciju po
Ako izraz gledamo kao kvadratnu funkciju po  , diskriminanta je jednaka
, diskriminanta je jednaka 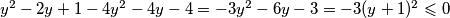 , pa je izraz uvijek veći ili jednak
, pa je izraz uvijek veći ili jednak  , kao što je i trebalo dokazati.
, kao što je i trebalo dokazati.
Četvrto rješenje. (Ivan Novak)
Ako je 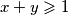 , onda je
, onda je 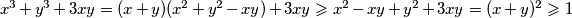 .
.
Ako je 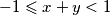 , onda je
, onda je 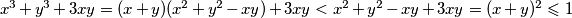 .
.
Ako je 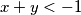 , razlikujemo
, razlikujemo  slučaja:
slučaja: 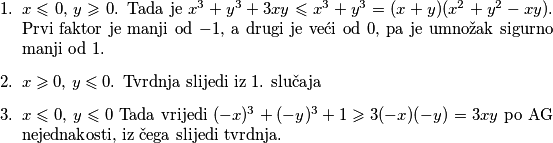
{ \textbf{Prvo rješenje. (Borna Šimić)}}
Prva nejednakost je $(x+y)^3\leqslant 1 \iff x+y \leqslant 1$.
Međutim, imamo \[ x^3 + y^3 - 1 + 3xy = \frac{1}{2}(x+y-1)((x-y)^2 + (x+1)^2 + (y+1)^2) \] pa su nejednakosti očito ekvivalentne.
{ \textbf{Drugo rješenje. (Ivan Novak)}}
Razlikujemo $4$ slučaja: \begin{enumerate}
\item $x\leqslant 0$, $y\leqslant 0$. Tada uvijek vrijedi $x+y\leqslant 1$, a vrijedi i $(-x)^3+(-y)^3+1\geqslant 3(-x)(-y)=3xy$ po AG nejednakosti.
\item $x\geqslant 0$, $y \geqslant 0$. Ako je $x\geqslant 1-y$, onda je $x^3+3xy+y^3\geqslant (1-y)^3+3(1-y)y+y^3=1$. \\ \vspace{2mm} Ako je $x< 1-y$, onda je $x^3+3xy+y^3< (1-y)^3+3(1-y)y+y^3=1$.
\item $x\geqslant 0$, $y\leqslant 0$. Neka je $z=-y$. \\ \vspace{2mm} Ako je $x-z \leqslant 1$, onda je $x\leqslant z+1$, pa je $x^3-3xz-z^3-1=x(x^2-3z)-z^3-1.$ \\ Ako je $x^2-3z\geqslant 0$, onda je taj izraz manji ili jednak $ (z+1)(x^2-3z-z^2+z-1)=(z+1)(x^2-(z+1)^2)\leqslant 0$. \\ Ako je $x^2-3z<0$, tada je $x(x^2-3z)-z^3-1\leqslant 0$ jer je svaki pribrojnik manji ili jednak $0$.\\ \vspace{2mm} Ako je $x-z>1$, onda je $x > z+1$, pa je $x^3-3xz-z^3-1=x(x^2-3z)-z^3-1.$ \\ Ako je $x^2-3z>0$, tada je $x(x^2-3z)-z^3-1>(z+1)(x^2-3z-z^2+z-1)=(z+1)(x^2-(z+1)^2)> 0$. \\ Ako je $x^2-3z\leqslant 0$, onda je $x^2\leqslant 3z \leqslant z^2+2z+1$, pa je $x\leqslant z+1$, što je kontradikcija.
\item $x\leqslant 0$, $y \geqslant 0$. Tvrdnja slijedi iz $3$. slučaja.
\end{enumerate}
{\textbf{Treće rješenje. (Ivan Novak)}}
Prva nejednakost je ekvivalentna s $x+y\leqslant 1$. Dovoljno je dokazati $(x+y-1)(x^3+y^3+3xy-1)\geqslant 0$. Sada vrijedi niz ekvivalencija: $$ (x+y-1)(x^3+y^3+3xy-1)\geqslant 0 \iff$$ $$ x^4+y^4+3x^2y+3xy^2+xy^3+yx^3+1-x^3-y^3-3xy-x-y \geqslant 0 \iff $$ $$ x^4+y^4+3x^2y+3xy^2+xy^3+yx^3+1 \geqslant x^3+y^3+3xy+x+y. $$ Uvedimo supstituciju $u=x+y$, $v=xy$. Tada zadnju nejednakost možemo zapisati kao $$ (x^2+y^2)^2-2x^2y^2+3xy(x+y)+(x+y)^2xy-2x^2y^2+1\geqslant (x+y)^3-3xy(x+y)+3xy+x+y \iff $$ $$ u^4+6uv+1 \geqslant u^3+3u^2v+3v+u \iff$$ $$u^4-u^3-u+1 \geqslant v(3+3u^2-6u) \iff$$ $$(u^3-1)(u-1)\geqslant 3v(u-1)^2 \iff$$ $$(u-1)^2(u^2+u+1)\geqslant 3v(u-1)^2 .$$ Ako je $u=1$, nejednakost je očita. Ako nije, tada je dovoljno pokazati $$u^2+u+1\geqslant 3v \iff x^2+y^2+2xy+x+y+1\geqslant 3xy \iff x^2+x(1-y)+y^2+y+1 \geqslant 0.$$ Ako izraz gledamo kao kvadratnu funkciju po $x$, diskriminanta je jednaka $y^2-2y+1-4y^2-4y-4=-3y^2-6y-3=-3(y+1)^2\leqslant 0$, pa je izraz uvijek veći ili jednak $0$, kao što je i trebalo dokazati.
{\textbf{Četvrto rješenje. (Ivan Novak)}}
Ako je $x+y\geqslant 1$, onda je $x^3+y^3+3xy=(x+y)(x^2+y^2-xy)+3xy\geqslant x^2-xy+y^2+3xy=(x+y)^2\geqslant 1$. \\ Ako je $-1\leqslant x+y <1$, onda je $x^3+y^3+3xy=(x+y)(x^2+y^2-xy)+3xy<x^2+y^2-xy+3xy=(x+y)^2\leqslant 1$. \\ Ako je $x+y<-1$, razlikujemo $3$ slučaja: \begin{enumerate}
\item $x\leqslant 0$, $y\geqslant 0$. Tada je $x^3+y^3+3xy\leqslant x^3+y^3=(x+y)(x^2+y^2-xy)$. Prvi faktor je manji od $-1$, a drugi je veći od $0$, pa je umnožak sigurno manji od $1$.
\item $x\geqslant 0$, $y\leqslant 0$. Tvrdnja slijedi iz $1$. slučaja
\item $x\leqslant 0$, $y\leqslant 0$ Tada vrijedi $(-x)^3+(-y)^3+1\geqslant 3(-x)(-y)=3xy$ po AG nejednakosti, iz čega slijedi tvrdnja.
\end{enumerate}
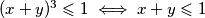 . Međutim, imamo
. Međutim, imamo 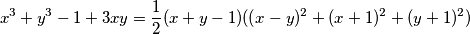 pa su nejednakosti očito ekvivalentne.
pa su nejednakosti očito ekvivalentne. slučaja:
slučaja: 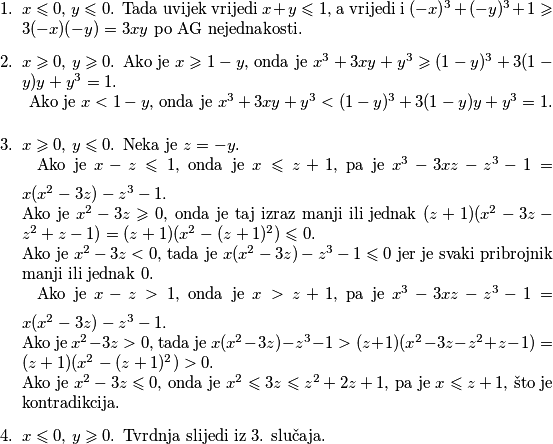
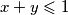 . Dovoljno je dokazati
. Dovoljno je dokazati 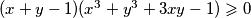 . Sada vrijedi niz ekvivalencija:
. Sada vrijedi niz ekvivalencija: 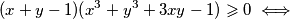
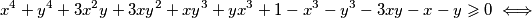
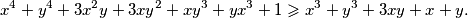 Uvedimo supstituciju
Uvedimo supstituciju 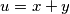 ,
, 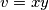 . Tada zadnju nejednakost možemo zapisati kao
. Tada zadnju nejednakost možemo zapisati kao 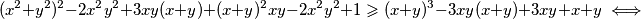
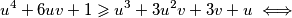
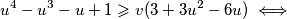
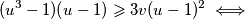
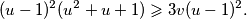 Ako je
Ako je 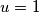 , nejednakost je očita. Ako nije, tada je dovoljno pokazati
, nejednakost je očita. Ako nije, tada je dovoljno pokazati 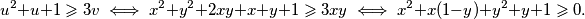 Ako izraz gledamo kao kvadratnu funkciju po
Ako izraz gledamo kao kvadratnu funkciju po  , diskriminanta je jednaka
, diskriminanta je jednaka 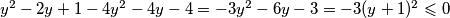 , pa je izraz uvijek veći ili jednak
, pa je izraz uvijek veći ili jednak  , kao što je i trebalo dokazati.
, kao što je i trebalo dokazati.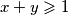 , onda je
, onda je 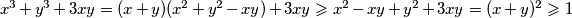 .
. 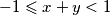 , onda je
, onda je 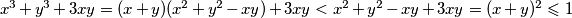 .
. 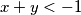 , razlikujemo
, razlikujemo  slučaja:
slučaja: 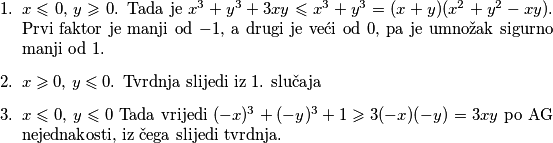
 Školjka
Školjka 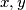 realni brojevi. Dokaži:
realni brojevi. Dokaži: