Prvo rješenje.
Označimo s  središte opisane kružnice, te s
središte opisane kružnice, te s  polovište stranice
polovište stranice  .
.
Neka je 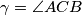 , te neka je
, te neka je 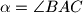 . Tada je
. Tada je 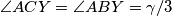 (obodni kutevi nad tetivom
(obodni kutevi nad tetivom 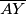 ). Nadalje, vrijedi
). Nadalje, vrijedi 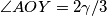 (središnji kut nad
(središnji kut nad 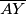 ). Kako je
). Kako je 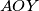 jednakokračan, vrijedi
jednakokračan, vrijedi 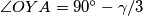 .
.
Trokutovi 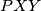 i
i 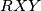 su sukladni jer su refleksija jedan drugog preko pravca
su sukladni jer su refleksija jedan drugog preko pravca  , pa vrijedi
, pa vrijedi 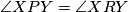 .
.
Trokut 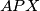 je jednakokračan, pa je
je jednakokračan, pa je 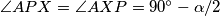 .
.
Četverokut 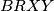 je tetivan ako i samo ako vrijedi
je tetivan ako i samo ako vrijedi 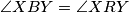 , jer su to obodni kutevi nad tetivom
, jer su to obodni kutevi nad tetivom 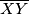 .
.
To vrijedi ako i samo ako vrijedi 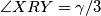 , što vrijedi ako i samo ako je
, što vrijedi ako i samo ako je 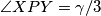 . Nadalje, to vrijedi ako i samo ako vrijedi
. Nadalje, to vrijedi ako i samo ako vrijedi 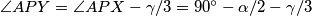 .
.
Kako je 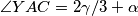 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 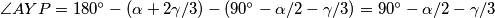 .
.
To vrijedi ako i samo ako je 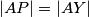 , a kako je
, a kako je 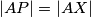 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 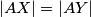 .
.
Središte kružnice opisane trokutu 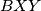 , nazovimo ga
, nazovimo ga  , je na
, je na  ako i samo ako vrijedi
ako i samo ako vrijedi 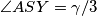 . Vrijedi
. Vrijedi 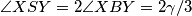 , pa je
, pa je 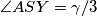 ako i samo ako je
ako i samo ako je 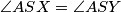 , a kako je
, a kako je 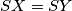 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 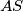 simetrala od
simetrala od 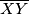 , što vrijedi ako i samo ako je
, što vrijedi ako i samo ako je 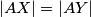 .
.
Drugo rješenje.
Pretpostavimo da je središte kružnice opisane trokutu 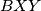 na
na  . Tada je to središte polovište kraćeg luka
. Tada je to središte polovište kraćeg luka 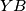 . Označimo ga s
. Označimo ga s  . Želimo dokazati
. Želimo dokazati 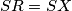 . Dovoljno je pokazati da je preslika
. Dovoljno je pokazati da je preslika  preko
preko  jednaka
jednaka  jer vrijedi
jer vrijedi 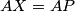 .
.
Vrijedi 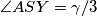 , ali i
, ali i 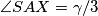 (obodni kutevi nad tetivama iste duljine). Iz ovog slijedi da su
(obodni kutevi nad tetivama iste duljine). Iz ovog slijedi da su 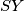 i
i 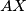 paralelni.
paralelni.
Nadalje, vrijedi 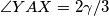 , te vrijedi
, te vrijedi 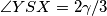 , pa su i
, pa su i 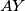 i
i 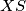 paralelni, pa je četverokut
paralelni, pa je četverokut 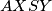 paralelogram, a kako je
paralelogram, a kako je 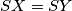 , vrijedi i
, vrijedi i 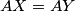 , četverokut je romb. Iz toga slijedi da je
, četverokut je romb. Iz toga slijedi da je  preslika
preslika  preko
preko  , pa vrijedi
, pa vrijedi 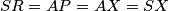 , kao što je i trebalo pokazati.
, kao što je i trebalo pokazati.
Pretpostavimo da je četverokut 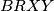 tetivan. Tada kao u prvom rješenju zaključujemo
tetivan. Tada kao u prvom rješenju zaključujemo 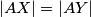 . Iz toga slijedi da je
. Iz toga slijedi da je 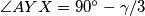 , ali vrijedi i
, ali vrijedi i 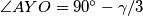 , pa su
, pa su 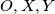 kolinearne.
kolinearne.
Iz toga slijedi da je  jednaka refleksiji preko
jednaka refleksiji preko  od
od  , pa je refleksija od
, pa je refleksija od  preko
preko  također na
također na  . Neka je
. Neka je 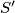 refleksija od
refleksija od  preko
preko  . Tada je
. Tada je 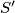 polovište kraćeg luka
polovište kraćeg luka 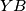 , pa vrijedi
, pa vrijedi 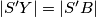 . Nadalje, iz
. Nadalje, iz 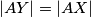 slijedi
slijedi 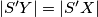 , pa je
, pa je 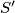 središte kružnice opisane trokutu
središte kružnice opisane trokutu 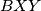 , kao što je i trebalo pokazati.
, kao što je i trebalo pokazati.
{\textbf{Prvo rješenje.}}
Označimo s $O$ središte opisane kružnice, te s $P$ polovište stranice $\overline{AC}$. \\
Neka je $\gamma=\angle ACB$, te neka je $\alpha=\angle BAC$. Tada je $\angle ACY=\angle ABY= \gamma/3$ (obodni kutevi nad tetivom $\overline{AY}$). Nadalje, vrijedi $\angle AOY= 2\gamma/3$ (središnji kut nad $\overline{AY}$). Kako je $AOY$ jednakokračan, vrijedi $\angle OYA=90^\circ-\gamma/3$. \\
Trokutovi $PXY$ i $RXY$ su sukladni jer su refleksija jedan drugog preko pravca $XY$, pa vrijedi $\angle XPY=\angle XRY$. \\ Trokut $APX$ je jednakokračan, pa je $\angle APX =\angle AXP= 90^\circ-\alpha/2$. \\
Četverokut $BRXY$ je tetivan ako i samo ako vrijedi $\angle XBY=\angle XRY$, jer su to obodni kutevi nad tetivom $\overline{XY}$. \\ To vrijedi ako i samo ako vrijedi $\angle XRY= \gamma/3$, što vrijedi ako i samo ako je $\angle XPY=\gamma/3$. Nadalje, to vrijedi ako i samo ako vrijedi $\angle APY= \angle APX - \gamma/3=90^\circ-\alpha/2-\gamma/3$. \\ Kako je $\angle YAC= 2\gamma/3+\alpha$, to vrijedi ako i samo ako je $\angle AYP =180^\circ-(\alpha+2\gamma/3)-(90^\circ-\alpha/2-\gamma/3)=90^\circ-\alpha/2-\gamma/3$. \\
To vrijedi ako i samo ako je $|AP|=|AY|$, a kako je $|AP|=|AX|$, to vrijedi ako i samo ako je $|AX|=|AY|$. \\
Središte kružnice opisane trokutu $BXY$, nazovimo ga $S$, je na $\Gamma$ ako i samo ako vrijedi $\angle ASY=\gamma/3$.
Vrijedi $\angle XSY= 2\angle XBY=2\gamma/3$, pa je $\angle ASY= \gamma/3$ ako i samo ako je $\angle ASX=\angle ASY$,
a kako je $SX=SY$, to vrijedi ako i samo ako je $AS$ simetrala od $\overline{XY}$, što vrijedi ako i samo ako je $|AX|=|AY|$. \\
{\textbf{Drugo rješenje.}}
Pretpostavimo da je središte kružnice opisane trokutu $BXY$ na $\Gamma$. Tada je to središte polovište kraćeg luka $YB$. Označimo ga s $S$. Želimo dokazati $SR=SX$.
Dovoljno je pokazati da je preslika $S$ preko $XY$ jednaka $A$ jer vrijedi $AX=AP$. \\ Vrijedi $\angle ASY= \gamma/3$, ali i $\angle SAX=\gamma/3$ (obodni kutevi nad tetivama iste duljine).
Iz ovog slijedi da su $SY$ i $AX$ paralelni. \\ Nadalje, vrijedi $\angle YAX=2\gamma/3$, te vrijedi $\angle YSX=2\gamma/3$, pa su i $AY$ i $XS$ paralelni, pa je četverokut $AXSY$ paralelogram,
a kako je $SX=SY$, vrijedi i $AX=AY$, četverokut je romb. Iz toga slijedi da je $A$ preslika $S$ preko $XY$, pa vrijedi $SR=AP=AX=SX$, kao što je i trebalo pokazati. \\
Pretpostavimo da je četverokut $BRXY$ tetivan. Tada kao u prvom rješenju zaključujemo $|AX|=|AY|$. Iz toga slijedi da je $\angle AYX=90^\circ-\gamma/3$, ali vrijedi i $\angle AYO=90^\circ-\gamma/3$,
pa su $O,X,Y$ kolinearne. \\
Iz toga slijedi da je $\Gamma$ jednaka refleksiji preko $XY$ od $\Gamma$, pa je refleksija od $A$ preko $XY$ također na $\Gamma$. Neka je $S'$ refleksija od $A$ preko $XY$.
Tada je $S'$ polovište kraćeg luka $YB$, pa vrijedi $|S'Y|=|S'B|$. Nadalje, iz $|AY|=|AX|$ slijedi $|S'Y|=|S'X|$, pa je $S'$ središte kružnice opisane trokutu $BXY$, kao što je i trebalo pokazati.
 u kojem vrijedi
u kojem vrijedi 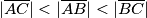 . Neka je
. Neka je  njegova opisana kružnica. Neka je
njegova opisana kružnica. Neka je  točka na
točka na  , na manjem luku
, na manjem luku 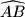 , takva da vrijedi
, takva da vrijedi 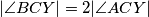 . Neka je
. Neka je  točka na stranici
točka na stranici  takva da vrijedi
takva da vrijedi 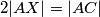 . Neka je
. Neka je  točka osnosimetrična polovištu dužine
točka osnosimetrična polovištu dužine  s obzirom na pravac
s obzirom na pravac  . Dokaži da kružnica opisana trokutu
. Dokaži da kružnica opisana trokutu 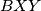 prolazi kroz
prolazi kroz  ako i samo ako joj je središte na
ako i samo ako joj je središte na  .
. središte opisane kružnice, te s
središte opisane kružnice, te s  polovište stranice
polovište stranice  .
. 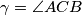 , te neka je
, te neka je 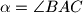 . Tada je
. Tada je 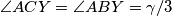 (obodni kutevi nad tetivom
(obodni kutevi nad tetivom 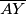 ). Nadalje, vrijedi
). Nadalje, vrijedi 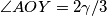 (središnji kut nad
(središnji kut nad 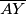 ). Kako je
). Kako je 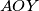 jednakokračan, vrijedi
jednakokračan, vrijedi 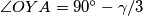 .
. 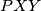 i
i 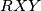 su sukladni jer su refleksija jedan drugog preko pravca
su sukladni jer su refleksija jedan drugog preko pravca  , pa vrijedi
, pa vrijedi 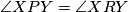 .
. 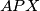 je jednakokračan, pa je
je jednakokračan, pa je 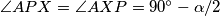 .
. 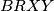 je tetivan ako i samo ako vrijedi
je tetivan ako i samo ako vrijedi 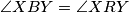 , jer su to obodni kutevi nad tetivom
, jer su to obodni kutevi nad tetivom 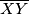 .
. 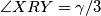 , što vrijedi ako i samo ako je
, što vrijedi ako i samo ako je 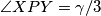 . Nadalje, to vrijedi ako i samo ako vrijedi
. Nadalje, to vrijedi ako i samo ako vrijedi 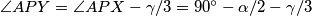 .
. 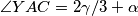 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 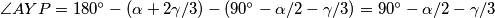 .
. 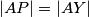 , a kako je
, a kako je 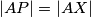 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 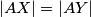 .
. 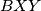 , nazovimo ga
, nazovimo ga  , je na
, je na  ako i samo ako vrijedi
ako i samo ako vrijedi 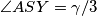 . Vrijedi
. Vrijedi 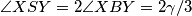 , pa je
, pa je 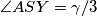 ako i samo ako je
ako i samo ako je 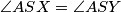 , a kako je
, a kako je 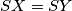 , to vrijedi ako i samo ako je
, to vrijedi ako i samo ako je 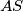 simetrala od
simetrala od 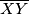 , što vrijedi ako i samo ako je
, što vrijedi ako i samo ako je 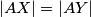 .
. 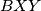 na
na  . Tada je to središte polovište kraćeg luka
. Tada je to središte polovište kraćeg luka 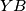 . Označimo ga s
. Označimo ga s  . Želimo dokazati
. Želimo dokazati 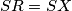 . Dovoljno je pokazati da je preslika
. Dovoljno je pokazati da je preslika  preko
preko  jednaka
jednaka  jer vrijedi
jer vrijedi 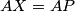 .
. 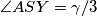 , ali i
, ali i 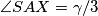 (obodni kutevi nad tetivama iste duljine). Iz ovog slijedi da su
(obodni kutevi nad tetivama iste duljine). Iz ovog slijedi da su 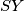 i
i 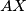 paralelni.
paralelni. 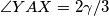 , te vrijedi
, te vrijedi 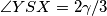 , pa su i
, pa su i 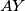 i
i 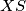 paralelni, pa je četverokut
paralelni, pa je četverokut 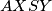 paralelogram, a kako je
paralelogram, a kako je 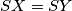 , vrijedi i
, vrijedi i 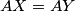 , četverokut je romb. Iz toga slijedi da je
, četverokut je romb. Iz toga slijedi da je  preslika
preslika  preko
preko  , pa vrijedi
, pa vrijedi 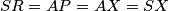 , kao što je i trebalo pokazati.
, kao što je i trebalo pokazati. 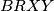 tetivan. Tada kao u prvom rješenju zaključujemo
tetivan. Tada kao u prvom rješenju zaključujemo 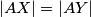 . Iz toga slijedi da je
. Iz toga slijedi da je 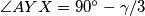 , ali vrijedi i
, ali vrijedi i 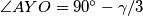 , pa su
, pa su 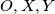 kolinearne.
kolinearne.  jednaka refleksiji preko
jednaka refleksiji preko  od
od  , pa je refleksija od
, pa je refleksija od  preko
preko  također na
također na  . Neka je
. Neka je 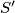 refleksija od
refleksija od  preko
preko  . Tada je
. Tada je 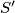 polovište kraćeg luka
polovište kraćeg luka 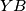 , pa vrijedi
, pa vrijedi 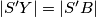 . Nadalje, iz
. Nadalje, iz 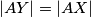 slijedi
slijedi 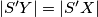 , pa je
, pa je 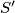 središte kružnice opisane trokutu
središte kružnice opisane trokutu 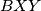 , kao što je i trebalo pokazati.
, kao što je i trebalo pokazati.  Školjka
Školjka