50%
19. travnja 2012. 13:16 (13 godine, 9 mjeseci)
Neka je skup prirodnih brojeva podijeljen u intervale na sljedeći način:
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.
a) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 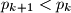 .
.
b) Dokaži ili opovrgni: Postoji beskonačno brojeva za koje je
za koje je 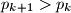 .
.
U prvom intervalu je broj 1, u drugom brojevi 2 i 3, u trećem 4, 5 i 6 i u svakom idućem jedan broj više nego u prethodnom (brojevi u intervalima su uzastopni).
Neka je
 udio prostih brojeva u
udio prostih brojeva u  -tom intervalu.
-tom intervalu.a) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 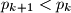 .
.b) Dokaži ili opovrgni: Postoji beskonačno brojeva
 za koje je
za koje je 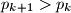 .
. Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Kliknite ovdje kako biste prikazali rješenje.
neka je 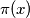 broj prostih brojeva u
broj prostih brojeva u  -tom intervalu...uvjet zadatka je ekvivalentan sa
-tom intervalu...uvjet zadatka je ekvivalentan sa
 postoji beskonacno mnogo brojeva
postoji beskonacno mnogo brojeva  za koje je
za koje je 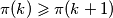

 potoji beskonacno mnogo brojeva
potoji beskonacno mnogo brojeva  za koje je
za koje je 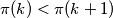

brojevi u -tom intervalu su
-tom intervalu su 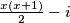 gdje
gdje 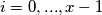
pa ako je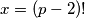 za neki prost broj
za neki prost broj  nijedan broj u
nijedan broj u  -tom intervalu nije prost- za
-tom intervalu nije prost- za 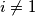 trivijalna faktorizacija, a za
trivijalna faktorizacija, a za 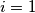 vrijedi
vrijedi 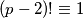
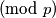 po Wilsonovom teoremu pa
po Wilsonovom teoremu pa 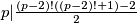
dokazimo prvo - pretpostavimo suprotno pa vrijedi izraz
- pretpostavimo suprotno pa vrijedi izraz  za svaki dovoljno veliki
za svaki dovoljno veliki 
no buduci da postoji beskonacno mnogo intervala bez prostih brojeva, nakon nekog vremena nece nijedan interval sadrzavati prost broj sto je u kontradikciji sa cinjenicom da postoji beskonacno mnogo prostih brojeva.
dokazimo sad -pretpostavimo suprotno i sad vrijedi izraz
-pretpostavimo suprotno i sad vrijedi izraz  za svaki dovoljno veliki
za svaki dovoljno veliki 
no to sad znaci da ce nakon nekog vremena se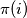 samo povecavati,te ce nakon nekog vremena prijeci polovicu velicine intervala jer se velicina intervala povecava za
samo povecavati,te ce nakon nekog vremena prijeci polovicu velicine intervala jer se velicina intervala povecava za  ... no polovica su parni brojevi i time dobivamo kontradikciju...
... no polovica su parni brojevi i time dobivamo kontradikciju...
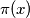 broj prostih brojeva u
broj prostih brojeva u  -tom intervalu...uvjet zadatka je ekvivalentan sa
-tom intervalu...uvjet zadatka je ekvivalentan sa postoji beskonacno mnogo brojeva
postoji beskonacno mnogo brojeva  za koje je
za koje je 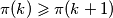

 potoji beskonacno mnogo brojeva
potoji beskonacno mnogo brojeva  za koje je
za koje je 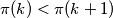

brojevi u
 -tom intervalu su
-tom intervalu su 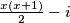 gdje
gdje 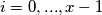
pa ako je
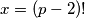 za neki prost broj
za neki prost broj  nijedan broj u
nijedan broj u  -tom intervalu nije prost- za
-tom intervalu nije prost- za 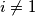 trivijalna faktorizacija, a za
trivijalna faktorizacija, a za 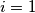 vrijedi
vrijedi 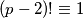
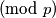 po Wilsonovom teoremu pa
po Wilsonovom teoremu pa 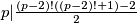
dokazimo prvo
 - pretpostavimo suprotno pa vrijedi izraz
- pretpostavimo suprotno pa vrijedi izraz  za svaki dovoljno veliki
za svaki dovoljno veliki 
no buduci da postoji beskonacno mnogo intervala bez prostih brojeva, nakon nekog vremena nece nijedan interval sadrzavati prost broj sto je u kontradikciji sa cinjenicom da postoji beskonacno mnogo prostih brojeva.
dokazimo sad
 -pretpostavimo suprotno i sad vrijedi izraz
-pretpostavimo suprotno i sad vrijedi izraz  za svaki dovoljno veliki
za svaki dovoljno veliki 
no to sad znaci da ce nakon nekog vremena se
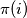 samo povecavati,te ce nakon nekog vremena prijeci polovicu velicine intervala jer se velicina intervala povecava za
samo povecavati,te ce nakon nekog vremena prijeci polovicu velicine intervala jer se velicina intervala povecava za  ... no polovica su parni brojevi i time dobivamo kontradikciju...
... no polovica su parni brojevi i time dobivamo kontradikciju... Ocjene: (2)
Komentari:
Buco, 20. travnja 2012. 13:19
Moguće da samo ja ne vidim ali kako ti točno radiš trivijalnu faktorizaciju za  različit od
različit od  mislim
mislim  ide od
ide od  do
do 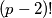 , a po meni tu može biti neki prosti broj veći od
, a po meni tu može biti neki prosti broj veći od 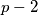 a time ti više nemaš trivijalnu faktorizaciju.
a time ti više nemaš trivijalnu faktorizaciju.
Čak ukoliko se ne varam znam dokazati da osim prvog intervala ne postoji niti jedan bez prostih brojeva što je doista i intuitivno jasno s obzirom da je gustoća prostih brojeva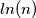 .
.
Moje rješenje zadatka je isto ko Bakićevo samo ja koristim umjesto Bertranda jednu poznatu nejednakost za prime counting function (koja se inače označava s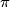 i označava broj prostih brojeva manjih od
i označava broj prostih brojeva manjih od  pa si me zbunio Ćevide)
pa si me zbunio Ćevide) 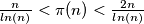 koja se lako dokaže ograničavanjem harmoničkog reda (da budemo iskreni vrijedi ovo gore, ali ja sam koristio nešto slabiju i lakšu za pokazati nejednakost za lijevu stranu, a desna mi treba samo da pokažem da nema nijedan interval s
koja se lako dokaže ograničavanjem harmoničkog reda (da budemo iskreni vrijedi ovo gore, ali ja sam koristio nešto slabiju i lakšu za pokazati nejednakost za lijevu stranu, a desna mi treba samo da pokažem da nema nijedan interval s  prostih, u rješenju izvornog zadatka je nepotrebna).
prostih, u rješenju izvornog zadatka je nepotrebna).
 različit od
različit od  mislim
mislim  ide od
ide od  do
do 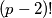 , a po meni tu može biti neki prosti broj veći od
, a po meni tu može biti neki prosti broj veći od 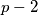 a time ti više nemaš trivijalnu faktorizaciju.
a time ti više nemaš trivijalnu faktorizaciju.Čak ukoliko se ne varam znam dokazati da osim prvog intervala ne postoji niti jedan bez prostih brojeva što je doista i intuitivno jasno s obzirom da je gustoća prostih brojeva
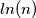 .
.Moje rješenje zadatka je isto ko Bakićevo samo ja koristim umjesto Bertranda jednu poznatu nejednakost za prime counting function (koja se inače označava s
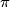 i označava broj prostih brojeva manjih od
i označava broj prostih brojeva manjih od  pa si me zbunio Ćevide)
pa si me zbunio Ćevide) 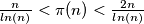 koja se lako dokaže ograničavanjem harmoničkog reda (da budemo iskreni vrijedi ovo gore, ali ja sam koristio nešto slabiju i lakšu za pokazati nejednakost za lijevu stranu, a desna mi treba samo da pokažem da nema nijedan interval s
koja se lako dokaže ograničavanjem harmoničkog reda (da budemo iskreni vrijedi ovo gore, ali ja sam koristio nešto slabiju i lakšu za pokazati nejednakost za lijevu stranu, a desna mi treba samo da pokažem da nema nijedan interval s  prostih, u rješenju izvornog zadatka je nepotrebna).
prostih, u rješenju izvornog zadatka je nepotrebna).  Školjka
Školjka