Neocijenjeno
5. kolovoza 2020. 20:05 (5 godine, 7 mjeseci)
Odredite najmanju i najveću moguću vrijednost izraza
$$\left( \frac{1}{a^2+1}+\frac{1}{b^2+1}+\frac{1}{c^2+1}\right)\left( \frac{a^2}{a^2+1}+\frac{b^2}{b^2+1}+\frac{c^2}{c^2+1}\right)$$
pri čemu su $a$, $b$ i $c$ nenegativni realni brojevi takvi da je $ab + bc + ca = 1$.
Upozorenje: Ovaj zadatak još niste riješili!
Kliknite ovdje kako biste prikazali rješenje.
Neka \(\sum\) označava cikličnu sumu te \(\prod\) ciklični produkt. Vrijedi:
\[\sum \frac{1}{a^2+1} = \sum \frac{1}{(a+b)(a+c)} = \frac{2(a+b+c)}{\prod (a+b)}\]
\[\sum \frac{a^2}{a^2+1} = \sum \frac{a^2}{(a+b)(a+c)} = \frac{\sum a^2(b+c)}{\prod (a+b)}\]
Pa je potrebno naći maksimum i minimum izraza
\[S = \frac{2(a+b+c)\sum a^2(b+c)}{\prod (a+b)^2}\]
Koristeći identitete \((a+b+c)(ab+bc+ac) = \sum a^2(b+c) + 3abc\) te \(\prod (a+b) = \sum a^2(b+c) + 2abc\) dobivamo:
\[S = \frac{2(\sum a^2(b+c) + 3abc)\sum a^2(b+c)}{(\sum a^2(b+c) + 2abc)^2}\]
Uvedimo oznake \(x = \sum a^2(b+c)\) i \(k = abc\). Primijetimo da zbog AG nejednakosti vrijedi \(x \geq 6k\). Sada lako dobivamo gornju granicu za \(S\):
\[S = \frac{2(x^2+3xk)}{x^2+4xk+4k^2} \leq \frac{2(x^2+4xk+4k^2)}{x^2+4xk+4k^2} = 2\]
Jednakost se postiže za \((a,b,c) = (1,1,0)\).\\
Odredimo sada minimalnu vrijednost od S. Vrijedi:
\[S = \frac{27}{16} \cdot \frac{32(x^2+3xk)}{27(x^2+4xk+4k^2)} = \frac{27}{16} \cdot \frac{27x^2+(5x^2+78xk) + 18xk}{27x^2+108xk+108k^2} \overset{x \geq 6k}{\geq} \frac{27}{16} \cdot \frac{27x^2+(30xk+78xk)+108k^2}{27x^2+108xk+108k^2} = \frac{27}{16}\]
Jednakost se postiže za \((a,b,c) = (\frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}}, \frac{1}{\sqrt{3}})\).
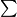 označava cikličnu sumu te
označava cikličnu sumu te 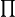 ciklični produkt. Vrijedi:
ciklični produkt. Vrijedi: 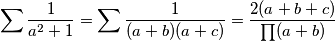
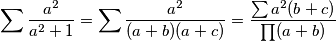 Pa je potrebno naći maksimum i minimum izraza
Pa je potrebno naći maksimum i minimum izraza 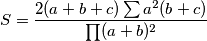 Koristeći identitete
Koristeći identitete 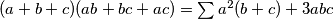 te
te 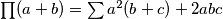 dobivamo:
dobivamo: 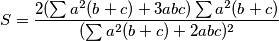 Uvedimo oznake
Uvedimo oznake 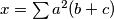 i
i 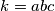 . Primijetimo da zbog AG nejednakosti vrijedi
. Primijetimo da zbog AG nejednakosti vrijedi 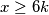 . Sada lako dobivamo gornju granicu za
. Sada lako dobivamo gornju granicu za 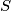 :
: 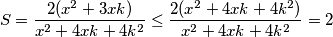 Jednakost se postiže za
Jednakost se postiže za 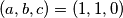 .
.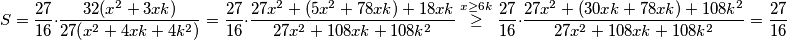 Jednakost se postiže za
Jednakost se postiže za 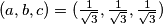 .
.  Školjka
Školjka 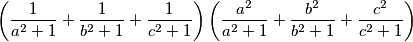 pri čemu su
pri čemu su  ,
,  i
i  nenegativni realni brojevi takvi da je
nenegativni realni brojevi takvi da je 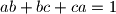 .
.