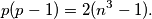Uočimo da s lijeve strane imamo 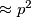 , a zdesne
, a zdesne 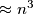 . Zato sigurno možemo ocijeniti veličinu
. Zato sigurno možemo ocijeniti veličinu  u odnosu na
u odnosu na  .
.
Naime, trivijalno imamo 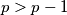 pa vrijedi
pa vrijedi 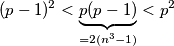 odnosno
odnosno 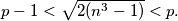 Sada se iz ovih jednadžbi lako dobija da vrijedi
Sada se iz ovih jednadžbi lako dobija da vrijedi 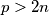 (uvjerite se sami).
(uvjerite se sami).
Kako  dijeli lijevu stranu jednadžbe, onda mora dijeliti i desnu stranu jednadžbe, odnosno,
dijeli lijevu stranu jednadžbe, onda mora dijeliti i desnu stranu jednadžbe, odnosno, 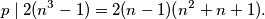 Naravno, kako je
Naravno, kako je 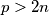 , znamo da
, znamo da 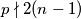 pa imamo
pa imamo 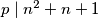 , to jest,
, to jest, 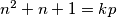 za neki prirodni broj
za neki prirodni broj  . Ako to vratimo u početnu jednadžbu, dobivamo
. Ako to vratimo u početnu jednadžbu, dobivamo 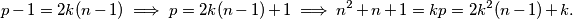 Nakon manjeg sređivanja, dobivamo
Nakon manjeg sređivanja, dobivamo 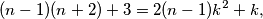 odnosno, kako
odnosno, kako  dijeli sve pribrojnike osim
dijeli sve pribrojnike osim 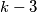 , mora dijeliti i
, mora dijeliti i 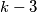 .
.
Sada ostaju dva slučaja, 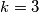 ili
ili 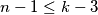 .
.
Ako je 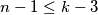 , dobivamo
, dobivamo 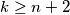 , odnosno, kako je
, odnosno, kako je 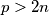 ,
, 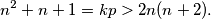 Rješavanjem ove nejednadžbe, vidimo da nema rješenja (provjerite).
Rješavanjem ove nejednadžbe, vidimo da nema rješenja (provjerite).
U drugom slučaju, imamo 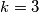 pa vrijedi
pa vrijedi 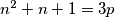 te
te 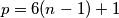 za što se opet lagano provjeri da nema rješenja (provjerite!!).
za što se opet lagano provjeri da nema rješenja (provjerite!!).
Naposljetku, kako smo završili sve slučajeve, znamo da jednadžba nema rješenja.
Uočimo da s lijeve strane imamo $\approx p^2$, a zdesne $\approx n^3$. Zato sigurno možemo ocijeniti veličinu $p$ u odnosu na $n$.
Naime, trivijalno imamo $p > p-1$ pa vrijedi
\[ (p-1)^2 < \underbrace{p(p-1)}_{=2(n^3-1)} < p^2 \] odnosno
\[ p - 1 < \sqrt{2(n^3-1)} < p .\] Sada se iz ovih jednadžbi lako dobija da vrijedi $p > 2n$ (uvjerite se sami).
Kako $p$ dijeli lijevu stranu jednadžbe, onda mora dijeliti i desnu stranu jednadžbe, odnosno, \[p \mid 2(n^3-1) = 2(n-1)(n^2+n+1).\] Naravno, kako je $p > 2n$, znamo da $p \nmid 2(n-1)$ pa imamo
$p \mid n^2 + n + 1$, to jest,
$n^2 + n + 1 = kp$ za neki prirodni broj $k$. Ako to vratimo u početnu jednadžbu, dobivamo \[p - 1 = 2k(n-1) \implies p = 2k(n-1) + 1 \implies n^2 + n + 1 = kp = 2k^2(n-1) + k. \] Nakon manjeg sređivanja, dobivamo
\[(n-1)(n+2) + 3 = 2(n-1)k^2 + k,\] odnosno, kako $n-1$ dijeli sve pribrojnike osim $k-3$, mora dijeliti i $k-3$.
Sada ostaju dva slučaja, $k = 3$ ili $n - 1 \leq k-3$.
Ako je $n - 1 \leq k -3$, dobivamo $k \geq n + 2$, odnosno, kako je $p > 2n$,
\[ n^2 + n + 1 = kp > 2n(n+2). \] Rješavanjem ove nejednadžbe, vidimo da nema rješenja (provjerite).
U drugom slučaju, imamo $k = 3$ pa vrijedi $n^2 + n + 1 = 3p$ te $p = 6(n-1) + 1$ za što se opet lagano provjeri da nema rješenja (provjerite!!).
Naposljetku, kako smo završili sve slučajeve, znamo da jednadžba nema rješenja.
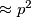 , a zdesne
, a zdesne 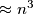 . Zato sigurno možemo ocijeniti veličinu
. Zato sigurno možemo ocijeniti veličinu  u odnosu na
u odnosu na  .
.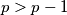 pa vrijedi
pa vrijedi 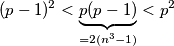 odnosno
odnosno 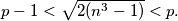 Sada se iz ovih jednadžbi lako dobija da vrijedi
Sada se iz ovih jednadžbi lako dobija da vrijedi 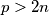 (uvjerite se sami).
(uvjerite se sami). dijeli lijevu stranu jednadžbe, onda mora dijeliti i desnu stranu jednadžbe, odnosno,
dijeli lijevu stranu jednadžbe, onda mora dijeliti i desnu stranu jednadžbe, odnosno, 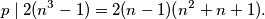 Naravno, kako je
Naravno, kako je 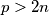 , znamo da
, znamo da 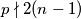 pa imamo
pa imamo 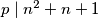 , to jest,
, to jest, 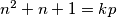 za neki prirodni broj
za neki prirodni broj  . Ako to vratimo u početnu jednadžbu, dobivamo
. Ako to vratimo u početnu jednadžbu, dobivamo 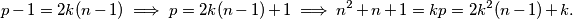 Nakon manjeg sređivanja, dobivamo
Nakon manjeg sređivanja, dobivamo 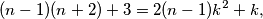 odnosno, kako
odnosno, kako  dijeli sve pribrojnike osim
dijeli sve pribrojnike osim 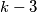 , mora dijeliti i
, mora dijeliti i 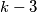 .
.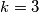 ili
ili 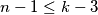 .
.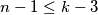 , dobivamo
, dobivamo 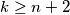 , odnosno, kako je
, odnosno, kako je 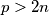 ,
, 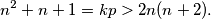 Rješavanjem ove nejednadžbe, vidimo da nema rješenja (provjerite).
Rješavanjem ove nejednadžbe, vidimo da nema rješenja (provjerite).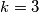 pa vrijedi
pa vrijedi 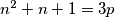 te
te 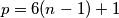 za što se opet lagano provjeri da nema rješenja (provjerite!!).
za što se opet lagano provjeri da nema rješenja (provjerite!!). Školjka
Školjka