Neka netko pogleda ovo, malo mi je sumnjivo: Reformulirat ćemo zadatak na sljedeći način: Neka je 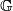 graf sa čvorovima
graf sa čvorovima 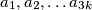 , te neka su
, te neka su  i
i 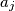 povezani crvenim bridom akko je
povezani crvenim bridom akko je 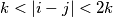 , inače su povezani plavom . Tvrdnja zadatka je da ne možemo odabrati
, inače su povezani plavom . Tvrdnja zadatka je da ne možemo odabrati 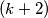 -člani podskup čvorova tako da nijedna 2 čvora nisu povezana.
-člani podskup čvorova tako da nijedna 2 čvora nisu povezana.
Ako pogledamo čvor 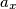 za bilo koji
za bilo koji  , razlikujemo 3 slučaja:
, razlikujemo 3 slučaja:
1. 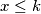
u tom slučaju su svi čvorovi sa kojima je spojen 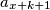 do
do 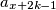 , odnosno ima ih
, odnosno ima ih 
2. 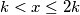
ako  zapišemo u obliku
zapišemo u obliku 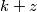 ,
, 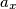 je povezan sa
je povezan sa  do
do 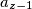 , te sa
, te sa 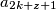 do
do 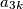 , odnosno ukupno
, odnosno ukupno 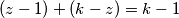
3. 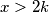
Neka je opet 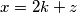 sada je
sada je 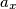 povezan sa
povezan sa 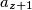 do
do 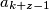 , odnosno
, odnosno  njih
njih
To znači da svaki čvor ima stupanj crvenih  . Također, za svaki čvor je jednistveno određen njegov skup čvorova s kojim je povezan bridom fiksne boje
. Također, za svaki čvor je jednistveno određen njegov skup čvorova s kojim je povezan bridom fiksne boje
pretpostavimo da je moguće odabrati takvih 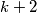 čvorova. Broj svih bridova je
čvorova. Broj svih bridova je 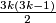 , a to možemo podijeliti na 3 klase:
, a to možemo podijeliti na 3 klase:
1. klasa obuhvaća plave bridove među odabranih 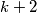 čvorova, njih ima
čvorova, njih ima 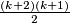
2. klasa obuhvaća sve crvene bridove, njih ima 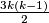
3. klasa sadržava sve ostale plave, kojih ima 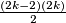
Zbrajanjem se dobiva:
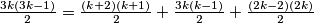 .
.
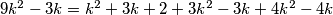
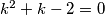
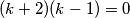
Pozitivno je rješenje 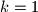 , ali kako je to protivno uvjetu zadatka, dobili smo kontradikciju, odnosno traženi odabir nije moguć, te smo gotovi
, ali kako je to protivno uvjetu zadatka, dobili smo kontradikciju, odnosno traženi odabir nije moguć, te smo gotovi
Neka netko pogleda ovo, malo mi je sumnjivo:
Reformulirat ćemo zadatak na sljedeći način:
Neka je $\mathbb{G}$ graf sa čvorovima $a_1, a_2, \dots a_{3k}$, te neka su $a_i$ i $a_j$ povezani crvenim bridom akko je $k<|i-j|<2k$, inače su povezani plavom . Tvrdnja zadatka je da ne možemo odabrati $(k+2)$-člani podskup čvorova tako da nijedna 2 čvora nisu povezana.\\
Ako pogledamo čvor $a_x$ za bilo koji $x$, razlikujemo 3 slučaja:\\
1. $x \leq k$\\
u tom slučaju su svi čvorovi sa kojima je spojen $a_{x+k+1}$ do $a_{x+2k-1}$, odnosno ima ih $k-1$
2. $k<x \leq 2k$\\
ako $x$ zapišemo u obliku $k+z$, $a_x$ je povezan sa $a_1$ do $a_{z-1}$, te sa $a_{2k+z+1}$ do $a_{3k}$, odnosno ukupno $(z-1)+(k-z)=k-1$
3. $x>2k$\\
Neka je opet $x=2k+z$
sada je $a_x$ povezan sa $a_{z+1}$ do $a_{k+z-1}$, odnosno $k-1$ njih
To znači da svaki čvor ima stupanj crvenih $k-1$. Također, za svaki čvor je jednistveno određen njegov skup čvorova s kojim je povezan bridom fiksne boje
pretpostavimo da je moguće odabrati takvih $k+2$ čvorova.
Broj svih bridova je $\frac{3k(3k-1)}{2}$, a to možemo podijeliti na 3 klase:\\
1. klasa obuhvaća plave bridove među odabranih $k+2$ čvorova, njih ima $\frac{(k+2)(k+1)}{2}$\\
2. klasa obuhvaća sve crvene bridove, njih ima $\frac{3k(k-1)}{2}$\\
3. klasa sadržava sve ostale plave, kojih ima $\frac {(2k-2)(2k)}{2}$\\
Zbrajanjem se dobiva:\\
$\frac{3k(3k-1)}{2} = \frac{(k+2)(k+1)}{2}+ \frac{3k(k-1)}{2}+\frac {(2k-2)(2k)}{2}$.\\
$9k^2-3k=k^2+3k+2+3k^2-3k+4k^2-4k$\\
$k^2+k-2=0$\\
$(k+2)(k-1)=0$\\
Pozitivno je rješenje $k=1$, ali kako je to protivno uvjetu zadatka, dobili smo kontradikciju, odnosno traženi odabir nije moguć, te smo gotovi
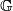 graf sa čvorovima
graf sa čvorovima 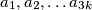 , te neka su
, te neka su  i
i 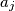 povezani crvenim bridom akko je
povezani crvenim bridom akko je 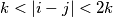 , inače su povezani plavom . Tvrdnja zadatka je da ne možemo odabrati
, inače su povezani plavom . Tvrdnja zadatka je da ne možemo odabrati 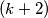 -člani podskup čvorova tako da nijedna 2 čvora nisu povezana.
-člani podskup čvorova tako da nijedna 2 čvora nisu povezana.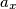 za bilo koji
za bilo koji  , razlikujemo 3 slučaja:
, razlikujemo 3 slučaja: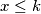
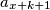 do
do 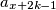 , odnosno ima ih
, odnosno ima ih 
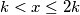
 zapišemo u obliku
zapišemo u obliku 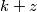 ,
, 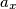 je povezan sa
je povezan sa  do
do 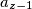 , te sa
, te sa 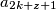 do
do 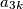 , odnosno ukupno
, odnosno ukupno 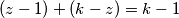
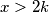
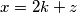 sada je
sada je 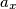 povezan sa
povezan sa 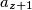 do
do 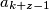 , odnosno
, odnosno  njih
njih . Također, za svaki čvor je jednistveno određen njegov skup čvorova s kojim je povezan bridom fiksne boje
. Također, za svaki čvor je jednistveno određen njegov skup čvorova s kojim je povezan bridom fiksne boje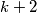 čvorova. Broj svih bridova je
čvorova. Broj svih bridova je 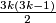 , a to možemo podijeliti na 3 klase:
, a to možemo podijeliti na 3 klase: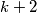 čvorova, njih ima
čvorova, njih ima 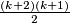
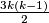
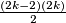
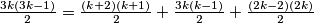 .
.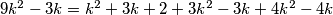
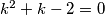
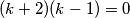
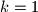 , ali kako je to protivno uvjetu zadatka, dobili smo kontradikciju, odnosno traženi odabir nije moguć, te smo gotovi
, ali kako je to protivno uvjetu zadatka, dobili smo kontradikciju, odnosno traženi odabir nije moguć, te smo gotovi  Školjka
Školjka  prirodan broj. Dano je
prirodan broj. Dano je 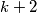 međusobno različitih prirodnih brojeva manjih od
međusobno različitih prirodnih brojeva manjih od 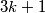 . Dokaži da među njima postoje dva čija je razlika veća od
. Dokaži da među njima postoje dva čija je razlika veća od 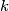 i manja od
i manja od 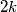 .
.